题目内容
(本小题满分14分高☆考♂资♀源*网)
证明以下命题:
对任一正整a,都存在整数b,c(b<c),使得![]() 成等差数列。
成等差数列。
存在无穷多个互不相似的三角形△![]() ,其边长
,其边长![]() 为正整数且
为正整数且![]() 成等差数列。
成等差数列。
【解析】作为压轴题,考查数学综合分析问题的能力以及创新能力。
(1)考虑到结构要证![]() ,;类似勾股数进行拼凑。
,;类似勾股数进行拼凑。
证明:考虑到结构特征,取特值![]() 满足等差数列,只需取b=5a,c=7a,对一切正整数a均能成立。
满足等差数列,只需取b=5a,c=7a,对一切正整数a均能成立。
结合第一问的特征,将等差数列分解,通过一个可做多种结构分解的因式说明构成三角形,再证明互不相似,且无穷。
证明:当![]() 成等差数列,则
成等差数列,则![]() ,
,
分解得:![]()
选取关于n的一个多项式,![]() 做两种途径的分解
做两种途径的分解
![]()
![]()
对比目标式,构造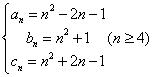 ,由第一问结论得,等差数列成立,
,由第一问结论得,等差数列成立,
考察三角形边长关系,可构成三角形的三边。
下证互不相似。
任取正整数m,n,若△m,△![]() 相似:则三边对应成比例
相似:则三边对应成比例![]() ,
,
由比例的性质得:![]() ,与约定不同的值矛盾,故互不相似。
,与约定不同的值矛盾,故互不相似。

 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案(本小题满分14分)
某研究机构为了研究人的脚的大小与身高之间的关系,随机抽测了20人,得到如下数据:
| 序 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 身高x(厘米) | 192 | 164 | 172 | 177 | 176 | 159 | 171 | 166 | 182 | 166 |
| 脚长y( 码 ) | 48 | 38 | 40 | 43 | 44 | 37 | 40 | 39 | 46 | 39 |
| 序 号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 身高x(厘米) | 169 | 178 | 167 | 174 | 168 | 179 | 165 | 170 | 162 | 170 |
| 脚长y( 码 ) | 43 | 41 | 40 | 43 | 40 | 44 | 38 | 42 | 39 | 41 |
(Ⅰ)若“身高大于175厘米”的为“高个”,“身高小于等于175厘米”的为“非高个”;“脚长大于42码”的为“大脚”,“脚长小于等于42码”的为“非大脚”.请根据上表数据完成下面的![]() 联列表:
联列表:
| 高 个 | 非高个 | 合 计 | |
| 大 脚 | |||
| 非大脚 | 12 | ||
| 合 计 | 20 |
(Ⅱ)根据题(1)中表格的数据,若按99%的可靠性要求,能否认为脚的大小与身高之间有关系?
(Ⅲ)若按下面的方法从这20人中抽取1人来核查测量数据的误差:将一个标有数字1,2,3,4,5,6的正六面体骰子连续投掷两次,记朝上的两个数字的乘积为被抽取人的序号.试求:
①抽到12号的概率;②抽到“无效序号(超过20号)”的概率.
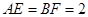 ,
,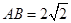 ,现将梯形沿CB、DA折起,使
,现将梯形沿CB、DA折起,使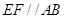 且
且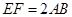 ,得一简单组合体
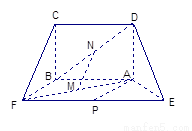
,得一简单组合体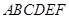 如图2示,已知
如图2示,已知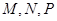 分别为
分别为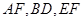 的中点.
的中点.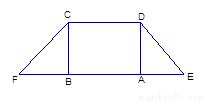
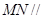 平面
平面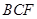 ;
;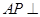
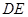 ;
; 多长时,平面
多长时,平面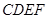 与平面
与平面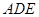 所成的锐二面角为
所成的锐二面角为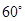 ?
?