题目内容
已知向量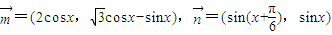 ,且满足
,且满足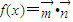 .
.(I)求函数y=f(x)的单调递增区间;
(II)设△ABC的内角A满足f(A)=2,且
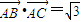 ,求边BC的最小值.
,求边BC的最小值.
【答案】分析:(I)根据向量的数量积公式和三角函数恒等变换的公式,化简得函数f(x)=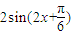 ,再由正弦函数的递增区间和整体思想进行求解;
,再由正弦函数的递增区间和整体思想进行求解;
(II)把条件代入(I)得到的解析式化简,再由A的范围和正弦值求出A,再代入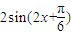 化简求出bc的值,结合余弦定理和基本不等式求出a的最小值.
化简求出bc的值,结合余弦定理和基本不等式求出a的最小值.
解答:解:(I)由题意得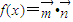 =2cosx
=2cosx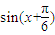 +(
+(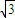 cosx-sinx)sinx
cosx-sinx)sinx
=2 sinxcosx+cos2x-sin2x=
sinxcosx+cos2x-sin2x=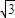 sin2x+cos2x
sin2x+cos2x
=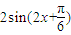 ,
,
由2kπ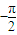 ≤
≤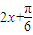 ≤2kπ
≤2kπ (k∈Z)得,
(k∈Z)得,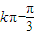 ≤x≤
≤x≤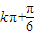 ,
,
则所求的单调递增区间是[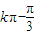 ,
,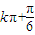 ](k∈Z).
](k∈Z).
(Ⅱ)由f(A)=2得,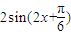 =2,即
=2,即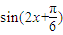 =1,
=1,
∵0<A<π,∴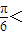 2A
2A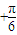
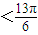 ,即2A
,即2A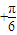 =
=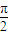 ,解得A=
,解得A=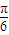 ,
,
由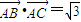 得,bccosA=
得,bccosA=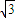 ,解得bc=2,
,解得bc=2,
在△ABC中,a2=b2+c2-2bccosA
=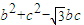
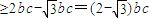 ,当且仅当b=c时取等号,
,当且仅当b=c时取等号,
∴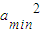 =
=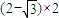 =4-2
=4-2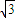 ,即a=
,即a=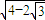 =
=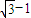 .
.
点评:本题考查了向量的数量积运算,三角函数恒等变换公式,以及余弦定理和基本不等式的综合应用,掌握正弦函数的基本性质和解析式正确化简,是解好本题的关键.
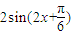 ,再由正弦函数的递增区间和整体思想进行求解;
,再由正弦函数的递增区间和整体思想进行求解;(II)把条件代入(I)得到的解析式化简,再由A的范围和正弦值求出A,再代入
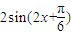 化简求出bc的值,结合余弦定理和基本不等式求出a的最小值.
化简求出bc的值,结合余弦定理和基本不等式求出a的最小值.解答:解:(I)由题意得
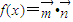 =2cosx
=2cosx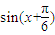 +(
+(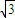 cosx-sinx)sinx
cosx-sinx)sinx=2
 sinxcosx+cos2x-sin2x=
sinxcosx+cos2x-sin2x=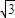 sin2x+cos2x
sin2x+cos2x=
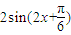 ,
,由2kπ
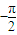 ≤
≤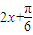 ≤2kπ
≤2kπ (k∈Z)得,
(k∈Z)得,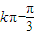 ≤x≤
≤x≤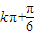 ,
,则所求的单调递增区间是[
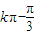 ,
,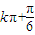 ](k∈Z).
](k∈Z).(Ⅱ)由f(A)=2得,
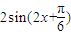 =2,即
=2,即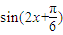 =1,
=1,∵0<A<π,∴
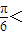 2A
2A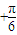
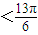 ,即2A
,即2A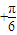 =
=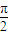 ,解得A=
,解得A=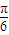 ,
,由
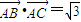 得,bccosA=
得,bccosA=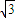 ,解得bc=2,
,解得bc=2,在△ABC中,a2=b2+c2-2bccosA
=
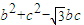
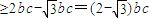 ,当且仅当b=c时取等号,
,当且仅当b=c时取等号,∴
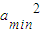 =
=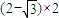 =4-2
=4-2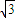 ,即a=
,即a=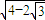 =
=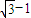 .
.点评:本题考查了向量的数量积运算,三角函数恒等变换公式,以及余弦定理和基本不等式的综合应用,掌握正弦函数的基本性质和解析式正确化简,是解好本题的关键.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
 ,
, 且满足
且满足 .
. 的解析式;
的解析式; 值;
值; 中,若
中,若 ,且
,且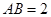 ,
, ,求
,求 的长.
的长.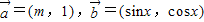 ,
,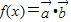 且满足
且满足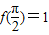 .
.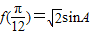 ,且AB=2,AC=3,求BC的长.
,且AB=2,AC=3,求BC的长.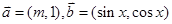 ,
,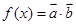 且满足
且满足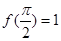 .
.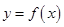 的解析式和单调增区间;
的解析式和单调增区间;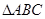 中,若
中,若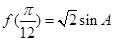 ,且
,且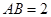 ,
,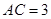 ,求
,求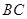 的长.
的长. ,且满足
,且满足 。
。 的坐标; (2)求向量
的坐标; (2)求向量 的夹角。
的夹角。