题目内容
(本题12分)
已知向量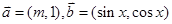 ,
,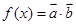 且满足
且满足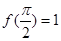 .
.
(1)求函数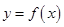 的解析式和单调增区间;
的解析式和单调增区间;
(2)锐角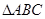 中,若
中,若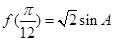 ,且
,且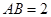 ,
,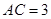 ,求
,求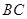 的长.
的长.
【答案】
(1)略
(2)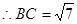
【解析】解(1)
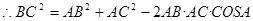
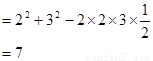
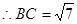

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
题目内容
(本题12分)
已知向量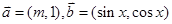 ,
,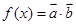 且满足
且满足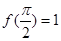 .
.
(1)求函数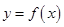 的解析式和单调增区间;
的解析式和单调增区间;
(2)锐角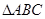 中,若
中,若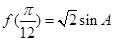 ,且
,且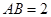 ,
,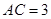 ,求
,求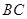 的长.
的长.
(1)略
(2)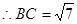
【解析】解(1)
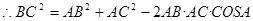
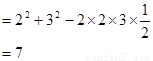
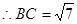

 巧学巧练系列答案
巧学巧练系列答案