题目内容
已知向量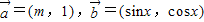 ,
,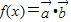 且满足
且满足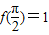 .
.(1)求函数y=f(x)的解析式;
(2)求函数y=f(x)的最小正周期、最值及其对应的x值;
(3)锐角△ABC中,若
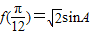 ,且AB=2,AC=3,求BC的长.
,且AB=2,AC=3,求BC的长.
【答案】分析:(1)利用向量数量积公式,结合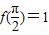 ,即可求函数y=f(x)的解析式;
,即可求函数y=f(x)的解析式;
(2)利用正弦函数的性质,即可求函数y=f(x)的最小正周期、最值及其对应的x值;
(3)先求A,再利用余弦定理,即可求BC的长.
解答:解:(1)∵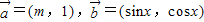 且
且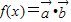
∴f(x)=msinx+cosx,
又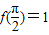 ,∴
,∴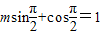 ,∴m=1,
,∴m=1,
∴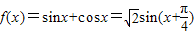 ;
;
(2)T=2π
当x=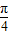 +2kπ(k∈Z)时,f(x)取得最大值为
+2kπ(k∈Z)时,f(x)取得最大值为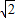 ;当x=
;当x=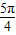 +2kπ(k∈Z)时,f(x)取得最小值为-
+2kπ(k∈Z)时,f(x)取得最小值为-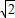 ;
;
(3)∵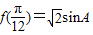 ,∴
,∴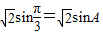
∵A是锐角△ABC的内角,∴A=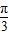
∵AB=2,AC=3,∴BC=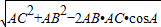 =
=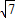 .
.
点评:本题考查向量知识的运用,考查正弦函数的性质,考查余弦定理,考查学生的计算能力,属于中档题.
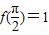 ,即可求函数y=f(x)的解析式;
,即可求函数y=f(x)的解析式;(2)利用正弦函数的性质,即可求函数y=f(x)的最小正周期、最值及其对应的x值;
(3)先求A,再利用余弦定理,即可求BC的长.
解答:解:(1)∵
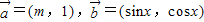 且
且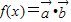
∴f(x)=msinx+cosx,
又
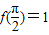 ,∴
,∴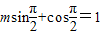 ,∴m=1,
,∴m=1,∴
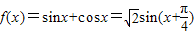 ;
;(2)T=2π
当x=
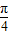 +2kπ(k∈Z)时,f(x)取得最大值为
+2kπ(k∈Z)时,f(x)取得最大值为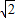 ;当x=
;当x=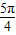 +2kπ(k∈Z)时,f(x)取得最小值为-
+2kπ(k∈Z)时,f(x)取得最小值为-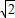 ;
;(3)∵
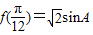 ,∴
,∴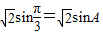
∵A是锐角△ABC的内角,∴A=
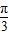
∵AB=2,AC=3,∴BC=
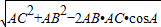 =
=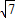 .
.点评:本题考查向量知识的运用,考查正弦函数的性质,考查余弦定理,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 ,
, 且满足
且满足 .
. 的解析式;
的解析式; 值;
值; 中,若
中,若 ,且
,且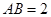 ,
, ,求
,求 的长.
的长.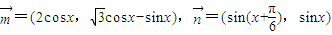 ,且满足
,且满足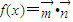 .
.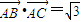 ,求边BC的最小值.
,求边BC的最小值.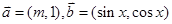 ,
,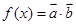 且满足
且满足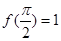 .
. 的解析式和单调增区间;
的解析式和单调增区间; 中,若
中,若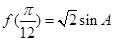 ,且
,且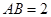 ,
,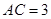 ,求
,求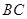 的长.
的长. ,且满足
,且满足 。
。 的坐标; (2)求向量
的坐标; (2)求向量 的夹角。
的夹角。