题目内容
已知m=50.6，n=0.65，p=lo
5，则m，n，p的大小关系为（ ）
| g | 0.6 |
| A、m＞n＞p |
| B、m＞p＞n |
| C、n＞m＞p |
| D、n＞p＞m |
分析：根据指数函数，幂函数和对数函数的性质分别判断取值范围即可．
解答：解：50.6＞1，0＜0.65＜1，log0.65＜0，
即m＞1，0＜n＜1，p＜0．
∴m＞n＞p，
故选：A．
即m＞1，0＜n＜1，p＜0．
∴m＞n＞p，
故选：A．
点评：本题主要考查函数值的大小比较，利用函数的性质是解决本题的关键．
练习册系列答案
相关题目
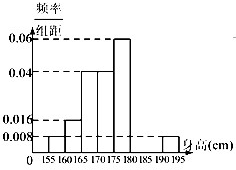从某校高三年级800名男生中随机抽取50名学生测量其身高，据测量被测学生的身高全部在155cm到195cm之间．将测量结果按如下方式分成8组：第一组[155，160），第二组[160，165），…，第八组[190，195]，如图是按上述分组得到的频率分布直方图的一部分．已知：第1组与第8组的人数相同，第6组、第7组和第8组的人数依次成等差数列．?（1）求下列频率分布表中所标字母的值，并补充完成频率分布直方图；
| 分组 | 频数 | 频率 | 频率/组距 |
| … | … | … | … |
| [180，185） | x | y | z |
| [185，190） | m | n | p |
| … | … | … | … |
右表是某班英语及数学成绩的分布表，已知该班有50名学生，成绩分1至5个档次．如：表中所示英语成绩为4分，数学成绩为2分的学生有5人．现设该班任意一位学生的英语成绩为m，数学成绩为n．
（1）求m=4，n=3的概率；
（2）求在m≥3的条件下，n=3的概率；
（3）求a+b的值，并求m的数学期望；
（4）若m=2与n=4是相互独立的，求a，b的值．
| n m |
数 学 | |||||
| 5 | 4 | 3 | 2 | 1 | ||
| 英 语 |
5 | 1 | 3 | 1 | 0 | 1 |
| 4 | 1 | 0 | 7 | 5 | 1 | |
| 3 | 2 | 1 | 0 | 9 | 3 | |
| 2 | 1 | b | 6 | 0 | a | |
| 1 | 0 | 0 | 1 | 1 | 3 | |
（2）求在m≥3的条件下，n=3的概率；
（3）求a+b的值，并求m的数学期望；
（4）若m=2与n=4是相互独立的，求a，b的值．
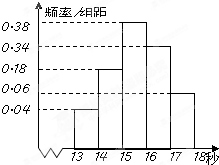（2011•西山区模拟）为调查某市学生百米运动成绩，从该市学生中按照男女生比例随机抽取50名学生进行百米测试，学生成绩全部都介于13秒到18秒之间，将测试结果按如下方式分成五组，第一组[13，14），第二组[14，15）…第五组[17，18]，如图是按上述分组方法得到的频率分布直方图．