题目内容
已知数列{an}的前n项和为Sn,且满足a1=a(a≠3),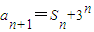 ,设
,设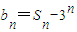 ,n∈N*.
,n∈N*.(1)求证:数列{bn}是等比数列;
(2)若an+1≥an,n∈N*,求实数a的最小值;
(3)当a=4时,给出一个新数列{en},其中
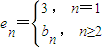 ,设这个新数列的前n项和为Cn,若Cn可以写成tp(t,p∈N*且t>1,p>1)的形式,则称Cn为“指数型和”.问{Cn}中的项是否存在“指数型和”,若存在,求出所有“指数型和”;若不存在,请说明理由.
,设这个新数列的前n项和为Cn,若Cn可以写成tp(t,p∈N*且t>1,p>1)的形式,则称Cn为“指数型和”.问{Cn}中的项是否存在“指数型和”,若存在,求出所有“指数型和”;若不存在,请说明理由.
【答案】分析:(1)依题意,可求得Sn+1=2Sn+3n,当a≠3时,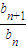 =2,利用等比数列的定义即可证得数列{bn}是等比数列;
=2,利用等比数列的定义即可证得数列{bn}是等比数列;
(2)由(1)可得Sn-3n=(a-3)×2n-1,an=Sn-Sn-1,n≥2,n∈N*,从而可求得an=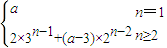 ,由an+1≥an,可求得a≥-9,从而可求得实数a的最小值;
,由an+1≥an,可求得a≥-9,从而可求得实数a的最小值;
(3)由(1)当a=4时,bn=2n-1,当n≥2时,Cn=3+2+4+…+2n=2n+1+1,C1=3,可证得对正整数n都有Cn=2n+1,依题意由tp=2n+1,tp-1=2n,(t,p∈N*且t>1,p>1),t只能是不小于3的奇数.分①当p为偶数时与②当p为奇数讨论即可得到答案.
解答:解:(1)an+1=Sn+3n⇒Sn+1=2Sn+3n,bn=Sn-3n,n∈N*,
当a≠3时,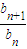 =
=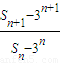 =
=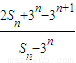 =2,
=2,
所以{bn}为等比数列.b1=S1-3=a-3,bn=(a-3)×2n-1.
(2)由(1)可得Sn-3n=(a-3)×2n-1,
an=Sn-Sn-1,n≥2,n∈N*,
∴an=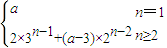 ,
,
∵an+1≥an,
∴a≥-9,又a≠3,
所以a的最小值为-9;
(3)由(1)当a=4时,bn=2n-1,
当n≥2时,Cn=3+2+4+…+2n=2n+1+1,C1=3,
所以对正整数n都有Cn=2n+1.
由tp=2n+1,tp-1=2n,(t,p∈N*且t>1,p>1),t只能是不小于3的奇数.
①当p为偶数时,tp-1=(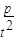 +1)(
+1)(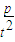 -1)=2n,
-1)=2n,
因为tp+1和tp-1都是大于1的正整数,
所以存在正整数g,h,使得tp+1=2g, -1=2h,2g-2h=2,2h(2g-h-1)=2,
-1=2h,2g-2h=2,2h(2g-h-1)=2,
所以2h=2且2g-h-1=1⇒h=1,g=2,相应的n=3,即有C3=32,C3为“指数型和”;
②当p为奇数时,tp-1=(t-1)(1+t+t2+…+tp-1),由于1+t+t2+…+tp-1是p个奇数之和,仍为奇数,又t-1为正偶数,
所以(t-1)(1+t+t2+…+tp-1)=2n不成立,此时没有“指数型和”.
点评:本题考查等差数列与等比数列的综合,考查数列求和,突出逻辑思维与创新思维、综合分析、运算能力的考查,属于难题.
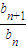 =2,利用等比数列的定义即可证得数列{bn}是等比数列;
=2,利用等比数列的定义即可证得数列{bn}是等比数列;(2)由(1)可得Sn-3n=(a-3)×2n-1,an=Sn-Sn-1,n≥2,n∈N*,从而可求得an=
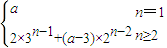 ,由an+1≥an,可求得a≥-9,从而可求得实数a的最小值;
,由an+1≥an,可求得a≥-9,从而可求得实数a的最小值;(3)由(1)当a=4时,bn=2n-1,当n≥2时,Cn=3+2+4+…+2n=2n+1+1,C1=3,可证得对正整数n都有Cn=2n+1,依题意由tp=2n+1,tp-1=2n,(t,p∈N*且t>1,p>1),t只能是不小于3的奇数.分①当p为偶数时与②当p为奇数讨论即可得到答案.
解答:解:(1)an+1=Sn+3n⇒Sn+1=2Sn+3n,bn=Sn-3n,n∈N*,
当a≠3时,
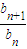 =
=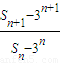 =
=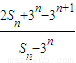 =2,
=2,所以{bn}为等比数列.b1=S1-3=a-3,bn=(a-3)×2n-1.
(2)由(1)可得Sn-3n=(a-3)×2n-1,
an=Sn-Sn-1,n≥2,n∈N*,
∴an=
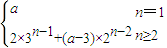 ,
,∵an+1≥an,
∴a≥-9,又a≠3,
所以a的最小值为-9;
(3)由(1)当a=4时,bn=2n-1,
当n≥2时,Cn=3+2+4+…+2n=2n+1+1,C1=3,
所以对正整数n都有Cn=2n+1.
由tp=2n+1,tp-1=2n,(t,p∈N*且t>1,p>1),t只能是不小于3的奇数.
①当p为偶数时,tp-1=(
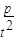 +1)(
+1)(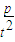 -1)=2n,
-1)=2n,因为tp+1和tp-1都是大于1的正整数,
所以存在正整数g,h,使得tp+1=2g,
 -1=2h,2g-2h=2,2h(2g-h-1)=2,
-1=2h,2g-2h=2,2h(2g-h-1)=2,所以2h=2且2g-h-1=1⇒h=1,g=2,相应的n=3,即有C3=32,C3为“指数型和”;
②当p为奇数时,tp-1=(t-1)(1+t+t2+…+tp-1),由于1+t+t2+…+tp-1是p个奇数之和,仍为奇数,又t-1为正偶数,
所以(t-1)(1+t+t2+…+tp-1)=2n不成立,此时没有“指数型和”.
点评:本题考查等差数列与等比数列的综合,考查数列求和,突出逻辑思维与创新思维、综合分析、运算能力的考查,属于难题.

练习册系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |