题目内容
设奇函数f(x)是定义在[-2,2]上的减函数,若f(1-m)<f(m),求实数m的取值范围.
分析:根据函数f(x)的奇偶性及单调性可去掉不等式中的符号“f”,从而化为具体不等式,注意考虑函数的定义域.
解答:解:∵奇函数f(x)是定义在[-2,2]上的减函数,
∴
,解得:-1≤m<
,
故所求m的取值范围是:{m|-1≤m<
}.
∴
|
| 1 |
| 2 |
故所求m的取值范围是:{m|-1≤m<
| 1 |
| 2 |
点评:本题考查函数的奇偶性、单调性及其应用,属基础题,抽象不等式的求解往往借助函数的单调性转化为具体不等式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
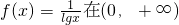 是减函数;
是减函数;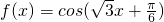 ,则f(x)+f'(x)是奇函数;
,则f(x)+f'(x)是奇函数;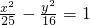 的一个焦点到渐近线的距离是5;
的一个焦点到渐近线的距离是5; 是减函数;
是减函数; ,则f(x)+f'(x)是奇函数;
,则f(x)+f'(x)是奇函数; 的一个焦点到渐近线的距离是5;
的一个焦点到渐近线的距离是5;