题目内容
(本小题满分12分,(Ⅰ)问5分,(Ⅱ)问7分)
设![]() 个不全相等的正数
个不全相等的正数![]() 依次围成一个圆圈.
依次围成一个圆圈.
(Ⅰ)若![]() ,且
,且![]() 是公差为
是公差为![]() 的等差数列,而
的等差数列,而![]() 是公比为
是公比为![]() 的等比数列;数列
的等比数列;数列![]() 的前
的前![]() 项和
项和![]() 满足:
满足:![]() ,求通项
,求通项![]() ;
;
(Ⅱ)若每个数![]() 是其左右相邻两数平方的等比中项,求证:
是其左右相邻两数平方的等比中项,求证:![]() ;
; ![]()
![]()
解析:(I)因![]() 是公比为d的等比数列,从而
是公比为d的等比数列,从而![]() 由
由![]() ,故
,故
解得![]() 或
或![]() (舍去)。因此
(舍去)。因此![]()
又 ![]() 。解得
。解得![]()
从而当![]() 时,
时,
![]()
当![]() 时,由
时,由![]() 是公比为d的等比数列得
是公比为d的等比数列得
![]()
因此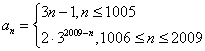
(II)由题意![]() 得
得
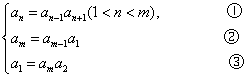
有①得![]() ④
④
由①,②,③得![]() ,
,
故![]() . ⑤
. ⑤
又![]() ,故有
,故有
![]() .⑥
.⑥
下面反证法证明:![]()
若不然,设![]()
若取![]() 即
即![]() ,则由⑥得
,则由⑥得![]() ,而由③得
,而由③得![]()
得![]() 由②得
由②得![]() 而
而
![]() ④及⑥可推得
④及⑥可推得![]() (
(![]() )与题设矛盾
)与题设矛盾
同理若P=2,3,4,5均可得![]() (
(![]() )与题设矛盾,因此
)与题设矛盾,因此![]() 为6的倍数
为6的倍数
由均值不等式得
![]()
由上面三组数内必有一组不相等(否则![]() ,从而
,从而![]() 与题设矛盾),故等号不成立,从而
与题设矛盾),故等号不成立,从而![]()
![]() 又
又![]() ,由④和⑥得
,由④和⑥得
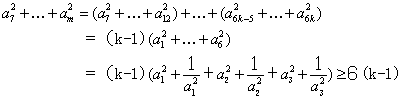
因此由⑤得
![]()

练习册系列答案
相关题目