题目内容
8.已知直线l:2x-y-1=0,动点P(x,y)在直线l上.(1)若A(0,4),B(-2,0),求|PA|+|PB|的最小值并求此时点P的坐标;
(2)若A(0,4),C(4,1),求|PC|-|PA|的最大值并求此时点P的坐际.
分析 (1)如图所示,设点A关于直线l的对称点A′(x,y),则$\left\{\begin{array}{l}{2×\frac{x+0}{2}-\frac{4+y}{2}-1=0}\\{\frac{y-4}{x-0}×2=-1}\end{array}\right.$,解得A′.连接A′B交直线l于点P,则点P即为所求.
(2)如图所示,由(1)可知:点A关于直线l的对称点A′(4,2),连接CA′并延长交直线l于点P,则点P满足使得|PC|-|PA|取得最大值|A′C|.
解答 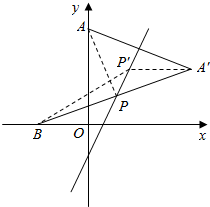 解:(1)如图所示,
解:(1)如图所示,
设点A关于直线l的对称点A′(x,y),
则$\left\{\begin{array}{l}{2×\frac{x+0}{2}-\frac{4+y}{2}-1=0}\\{\frac{y-4}{x-0}×2=-1}\end{array}\right.$,解得A′(4,2).
连接A′B交直线l于点P,则点P即为所求.
否则在直线l上除了点P以外的任取点P′,则BP′+AP′>A′B=BP+AP.
∴|PA|+|PB|的最小值=|BA′|=$\sqrt{{6}^{2}+{2}^{2}}$=2$\sqrt{10}$.
直线BA′:$y=\frac{0-2}{-2-4}(x+2)$,化为x-3y+2=0.
联立$\left\{\begin{array}{l}{x-3y+2=0}\\{2x-y-1=0}\end{array}\right.$,解得P(1,1).
(2)如图所示,
由(1)可知:点A关于直线l的对称点A′(4,2),
连接CA′并延长交直线l于点P(4,7),
则点P满足使得|PC|-|PA|取得最大值|A′C|=1.
否则在直线l上除了点P以外的任取点P′,则|P′C|-|P′A|<|A′C|.
∴P(4,7)满足使得|PC|-|PA|取得最大值|A′C|=1.
点评 本题考查了轴对称问题、线段的垂直平分线性质、三角形三边大小关系,考查了数形结合能力、推理能力与计算能力,属于中档题.

| A. | a<0,b<0,c<0 | B. | a<0,b≥0,c>0 | C. | 2-a<2c | D. | 2a+2c<2 |