题目内容
【题目】中央政府为了应对因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”,为了了解人们对“延迟退休年龄政策”的态度,责成人社部进行调研,人社部从网上年龄在![]() 岁的人群中随机调查100人,调查数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:
岁的人群中随机调查100人,调查数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:
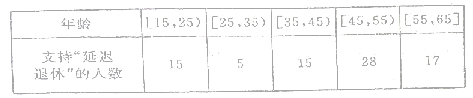
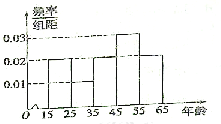
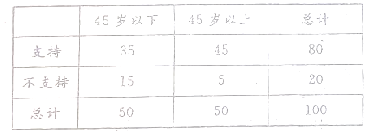
(1)由以上统计数据填![]() 列联表,并判断是否95%的把握认为以
列联表,并判断是否95%的把握认为以![]() 岁为界点的不同人群对“延迟退休年龄政策”的支持有差异;
岁为界点的不同人群对“延迟退休年龄政策”的支持有差异;

(2)若以![]() 岁为分界点,从不支持“延迟退休”的人中按分层抽样的方法抽取
岁为分界点,从不支持“延迟退休”的人中按分层抽样的方法抽取![]() 人参加某项活动,现从这
人参加某项活动,现从这![]() 人中随机抽
人中随机抽![]() 人.
人.
①抽到![]() 人是
人是![]() 岁以下时,求抽到的另一人是
岁以下时,求抽到的另一人是![]() 岁以上的概率;
岁以上的概率;
②记抽到![]() 岁以上的人数为
岁以上的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
|
|
|
|
|
|
|
|
|
|
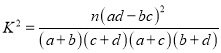
【答案】(1)有![]() 的把握(2)①
的把握(2)①![]() ②见解析
②见解析
【解析】试题分析:(1)由所给表格和频率分布直方图填出列联表,进一步求出![]() ,利用所给数据结合独立性检验内容可得结论;(2)利用古典概型可求抽到
,利用所给数据结合独立性检验内容可得结论;(2)利用古典概型可求抽到![]() 人是
人是![]() 岁以下时,抽一的另一人是
岁以下时,抽一的另一人是![]() 岁以上的概率,对于
岁以上的概率,对于![]() ,写出其所有可能取值,求出对应概率,做出分布列,再求出数学期.试题解析:
,写出其所有可能取值,求出对应概率,做出分布列,再求出数学期.试题解析:
因为![]() ,
,
所以有![]() 的把握认为以
的把握认为以![]() 岁为分界点的不同人群对“延迟退休政策”的支持度有差异.
岁为分界点的不同人群对“延迟退休政策”的支持度有差异.
(2)①抽到1人是![]() 岁以下的概率
岁以下的概率![]() ,抽到1人 以上的应抽
,抽到1人 以上的应抽![]() 人,故所求概率为
人,故所求概率为![]() .
.
则![]() ,
,
![]() ,
,
可得随机变量![]() 的分布列为
的分布列为
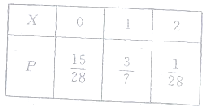
故数学期望为![]() .
.

练习册系列答案
相关题目