题目内容
15．已知集合A={（x，y）||x|+|y|≤1}，B={（x，y）|x2+y2≤1}，C={（x，y）||x|≤1，|y|≤1}，判断A、B、C之间的包含关系．分析 作出集合A，B，C的几何意义，从而判断三个集合的关系即可．
解答 解：作出集合A，B，C的几何意义如下，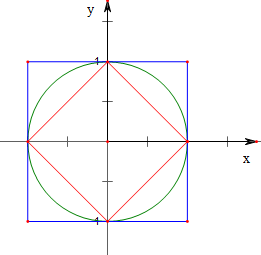
红色正方形内的所有的点是A，
绿色圆内的所有的点是B，
蓝色正方形内的所有的点是C，
故A?B?C．
点评 本题考查了集合的几何意义的应用及集合的关系的判断，属于基础题．
练习册系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
5．某研究小组为了研究中学生的身体发育情况，在某学校随机抽出20名15至16周岁的男生，将他们的身高和体重制成2×2的列联表，根据列联表的数据，判断该学校15至16周岁的男生的身高和体重之间在犯错误概率不超过0.025的前提下有关系．
附：独立性检验临界值表
k2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$．
| 超重 | 不超重 | 总计 | |
| 偏高 | 1 | 1 | 5 |
| 不偏高 | 3 | 12 | 15 |
| 总计 | 7 | 12 | 20 |
| P（K2≥k） | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |