题目内容
已知函数f(x)=ax•lnx+b(a,b∈R),在点(e,f(e))处的切线方程是2x-y-e=0(e为自然对数的底).(1)求实数a,b的值及f(x)的解析式;
(2)若t是正数,设h(x)=f(x)+f(t-x),求h(x)的最小值;
(3)若关于x的不等式xlnx+(6-x)ln(6-x)≥ln(k2-72k)对一切x∈(0,6)恒成立,求实数k的取值范围.
【答案】分析:(1)根据函数在点(e,f(e))处的切线方程是2x-y-e=0,可得f(e)=e,f′(e)=2,利用点(e,f(e))在函数f(x)=ax•lnx+b上,即可求实数a,b的值及f(x)的解析式;
(2)h(x)=f(x)+f(t-x)=xlnx+(t-x)ln(t-x),h(x)的定义域为(0,t),确定函数的单调性,从而可求h(x)的最小值;
(3)xlnx+(6-x)ln(6-x)=f(x)+f(6-x)=h(x),t=6时h(x)min=h(3)=6ln3=ln729,从而关于x的不等式xlnx+(6-x)ln(6-x)≥ln(k2-72k)对一切x∈(0,6)恒成立,转化为ln(k2-72k)≤ln729,解不等式,即可求得实数k的取值范围.
解答:解:(1)依题意有2e-f(e)-e=0,∴f(e)=e
∵f(x)=ax•lnx+b,∴f′(x)=alnx+a+b
∴f′(e)=alne+a+b=2,∴2a+b=2,∴b=2-2a
∵点(e,f(e))在函数f(x)=ax•lnx+b上
∴f(e)=aelne+b=ae+b=e
∴ae+2-2a=e,∴a=1
∴b=0,∴f(x)=xlnx;
故实数a=1,b=0,f(x)=xlnx …(4分)
(2)h(x)=f(x)+f(t-x)=xlnx+(t-x)ln(t-x),h(x)的定义域为(0,t);…(5分)
h′(x)=lnx+1-[ln(t-x)+1]=ln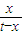 …(6分)
…(6分)
由h′(x)>0得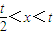 ;h′(x)<0得
;h′(x)<0得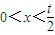 …(8分)
…(8分)
∴h(x)在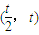 上是增函数,在(0,
上是增函数,在(0, )上是减函数
)上是减函数
∴h(x)min=h( )=tln
)=tln …(10分)
…(10分)
(3)∵xlnx+(6-x)ln(6-x)=f(x)+f(6-x)=h(x)
由(2)知,h(x)min=h( )=tln
)=tln ,∴t=6,h(x)min=h(3)=6ln3=ln729
,∴t=6,h(x)min=h(3)=6ln3=ln729
∵关于x的不等式xlnx+(6-x)ln(6-x)≥ln(k2-72k)对一切x∈(0,6)恒成立,
∴ln(k2-72k)≤ln729
∴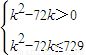
∴-9≤k<0或72<k≤81…(13分)
故实数k的取值范围为[-9,0)∪(72,81].…(14分)
点评:本题考查导数知识的运用,考查函数的单调性,考查函数的最值,考查恒成立问题,解题的关键是正确求导,确定函数的单调性,属于中档题.
(2)h(x)=f(x)+f(t-x)=xlnx+(t-x)ln(t-x),h(x)的定义域为(0,t),确定函数的单调性,从而可求h(x)的最小值;
(3)xlnx+(6-x)ln(6-x)=f(x)+f(6-x)=h(x),t=6时h(x)min=h(3)=6ln3=ln729,从而关于x的不等式xlnx+(6-x)ln(6-x)≥ln(k2-72k)对一切x∈(0,6)恒成立,转化为ln(k2-72k)≤ln729,解不等式,即可求得实数k的取值范围.
解答:解:(1)依题意有2e-f(e)-e=0,∴f(e)=e
∵f(x)=ax•lnx+b,∴f′(x)=alnx+a+b
∴f′(e)=alne+a+b=2,∴2a+b=2,∴b=2-2a
∵点(e,f(e))在函数f(x)=ax•lnx+b上
∴f(e)=aelne+b=ae+b=e
∴ae+2-2a=e,∴a=1
∴b=0,∴f(x)=xlnx;
故实数a=1,b=0,f(x)=xlnx …(4分)
(2)h(x)=f(x)+f(t-x)=xlnx+(t-x)ln(t-x),h(x)的定义域为(0,t);…(5分)
h′(x)=lnx+1-[ln(t-x)+1]=ln
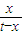 …(6分)
…(6分)由h′(x)>0得
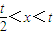 ;h′(x)<0得
;h′(x)<0得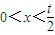 …(8分)
…(8分)∴h(x)在
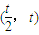 上是增函数,在(0,
上是增函数,在(0, )上是减函数
)上是减函数∴h(x)min=h(
 )=tln
)=tln …(10分)
…(10分)(3)∵xlnx+(6-x)ln(6-x)=f(x)+f(6-x)=h(x)
由(2)知,h(x)min=h(
 )=tln
)=tln ,∴t=6,h(x)min=h(3)=6ln3=ln729
,∴t=6,h(x)min=h(3)=6ln3=ln729∵关于x的不等式xlnx+(6-x)ln(6-x)≥ln(k2-72k)对一切x∈(0,6)恒成立,
∴ln(k2-72k)≤ln729
∴
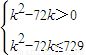
∴-9≤k<0或72<k≤81…(13分)
故实数k的取值范围为[-9,0)∪(72,81].…(14分)
点评:本题考查导数知识的运用,考查函数的单调性,考查函数的最值,考查恒成立问题,解题的关键是正确求导,确定函数的单调性,属于中档题.

练习册系列答案
相关题目