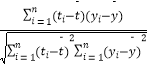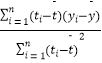题目内容
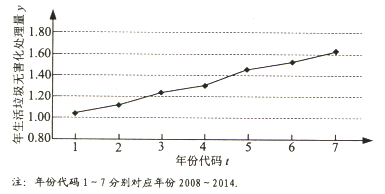
【题目】已知f（x）是定义在R上的偶函数，且x≤0时，f（x）=log 
（﹣x+1）．
（1）求f（x）的解析式；
（2）若f（a﹣1）＜﹣1，求实数a的取值范围．
【答案】
（1）解：令x＞0，则﹣x＜0，f（﹣x）=log 
（x+1）=f（x）
∴x＞0时，f（x）=log （x+1），
则f（x）= 
（2）解：∵f（x）=log （﹣x+1）在（﹣∞，0]上为增函数，
∴f（x）在（0，+∞）上为减函数
∵f（a﹣1）＜﹣1=f（1）
∴|a﹣1|＞1，
∴a＞2或a＜0
【解析】（1）根据函数奇偶性的性质即可求函数f（x）的解析式；（2）若f（a﹣1）＜﹣1，将不等式进行转化即可求实数a的取值范围
【考点精析】本题主要考查了对数函数的单调性与特殊点的相关知识点，需要掌握过定点（1，0），即x=1时，y=0;a>1时在（0，+∞）上是增函数;0>a>1时在（0，+∞）上是减函数才能正确解答此题．
练习册系列答案
相关题目
