题目内容
【题目】设函数![]() ,
, ![]() 为曲线
为曲线![]() 在点
在点![]() 处的切线.
处的切线.
(Ⅰ)求![]() 的方程.
的方程.
(Ⅱ)当![]() 时,证明:除切点
时,证明:除切点![]() 之外,曲线
之外,曲线![]() 在直线
在直线![]() 的下方.
的下方.
(Ⅲ)设![]() ,
, ![]() ,
, ![]() ,且满足
,且满足![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(Ⅰ)![]() (Ⅱ)见解析(Ⅲ)
(Ⅱ)见解析(Ⅲ)![]() .
.
【解析】试题分析:(Ⅰ)先求导,再求![]() 的值,根据导数的几何意义可知切线的斜率即为
的值,根据导数的几何意义可知切线的斜率即为![]() .由点斜式可得直线方程.(Ⅱ)即证明
.由点斜式可得直线方程.(Ⅱ)即证明![]() ,
, ![]() 恒成立.变形可得即证
恒成立.变形可得即证![]() 恒成立即可.令
恒成立即可.令![]() 求导,讨论导数的正负,根据导数的正负可得函数
求导,讨论导数的正负,根据导数的正负可得函数![]() 的单调性.根据单调性可求其最值,其最大值小于0即可.(Ⅲ)当
的单调性.根据单调性可求其最值,其最大值小于0即可.(Ⅲ)当![]() 且
且![]() 时由(Ⅱ)可知
时由(Ⅱ)可知![]() .当
.当![]() 中至少有一个大于等于
中至少有一个大于等于![]() 时,可用配方法求各自值域再相加.
时,可用配方法求各自值域再相加.
试题解析:解:(Ⅰ) 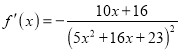 .
.
所以![]() .
.
所以 L的方程为![]() ,即
,即![]() . 3分
. 3分
(Ⅱ)要证除切点![]() 之外,曲线C在直线L的下方,只需证明
之外,曲线C在直线L的下方,只需证明![]() ,
, ![]() 恒成立.
恒成立.
因为![]() ,
,
所以只需证明![]() ,
, ![]() 恒成立即可. 5分
恒成立即可. 5分
设![]()
则![]() .
.
令![]() ,解得
,解得![]() ,
, ![]() . 6分
. 6分
当![]() 在
在![]() 上变化时,
上变化时, ![]() 的变化情况如下表
的变化情况如下表

所以![]() ,
, ![]() 恒成立. 8分
恒成立. 8分
(Ⅲ)(ⅰ)当![]() 且
且![]() 时,
时,
由(Ⅱ)可知: ![]() ,
,
![]() ,
, ![]() .
.
三式相加,得![]() .
.
因为![]() ,
,
所以![]() ,且当
,且当![]() 时取等号. 11分
时取等号. 11分
(ⅱ)当![]() 中至少有一个大于等于
中至少有一个大于等于![]() 时,
时,
不妨设![]() ,则
,则![]() ,
,
因为![]() ,
, ![]() ,
,
所以![]() .
.
综上所述,当![]() 时
时![]() 取到最大值
取到最大值![]() . 14分
. 14分

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目