题目内容

19．将x1，x2，…，xn中的最小数记为min{x1，x2…，xn}，最大数记为max{x1，x2…，xn}，则max{min{x2-4x+4，2x-1，-x+8}}（x∈R）的值为（　　）
A．1B．2C．4D．6

分析 在同一坐标系中作出三个函数y=2x-1，y=x2-4x+4与y=-x+8的图象，依题意，即可求得max{min{x2-4x+4，2x-1，-x+8}}（x∈R）的值．

解答 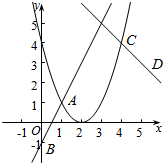解：在同一坐标系中
作出三个函数y=2x-1，y=x2-4x+4与y=-x+8的图象如图
由图可知，min{x2-4x+4，2x-1，-x+8}为射线AB，
抛物线弧AC，与射线CD的组合体，
显然，在C点时，y=min{x2-4x+4，2x-1，-x+8}取得最大值．
解方程组$\left\{\begin{array}{l}{y=-x+8}\\{y={x}^{2}-4x+4}\end{array}\right.$得，C（4，4），
∴max{min{x2-4x+4，2x-1，-x+8}}=4．
故选：C．

点评 本题考查函数的最值及其几何意义，注意运用数形结合的思想方法，正确理解新定义是解题的关键，属于中档题．

练习册系列答案
相关题目
9．如图给出了一个算法流程图，该算法流程图的功能是（　　）
A．求三个数中最大的数B．求三个数中最小的数
C．按从小到大排列D．按从大到小排列
10．已知平面向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$满足$\overrightarrow{c}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$（x，y∈R），且$\overrightarrow{a}$•$\overrightarrow{c}$＞0，$\overrightarrow{b}$•$\overrightarrow{c}$＞0．（　　）
A．若$\overrightarrow{a}$•$\overrightarrow{b}$＜0，则x＞0，y＞0B．若$\overrightarrow{a}$•$\overrightarrow{b}$＜0，则x＜0，y＜0
C．若$\overrightarrow{a}$•$\overrightarrow{b}$＞0，则x＜0，y＜0D．若$\overrightarrow{a}$•$\overrightarrow{b}$＞0，则x＞0，y＞0
7．已知函数f（x）=sin（2x-$\frac{π}{3}$），x∈R．求：
（1）函数f（x）在区间[0，π）内的一条对称轴；
（2）函数f（x）在区间[$\frac{π}{6}$，$\frac{2π}{3}$]上的最大值和最小值．
14．设A=$[\begin{array}{l}{3}&{7}&{-3}\\{-2}&{-5}&{2}\\{-4}&{-10}&{3}\end{array}]$，求AA*．
4．化简求值：
（1）${π^0}-{（\sqrt{8}）^{\frac{2}{3}}}+{0.0081^{\frac{1}{4}}}+\sqrt{2}•\root{3}{2}•\root{6}{2}$．
（2）（lg5）2+lg2•lg50+e2ln2+log28．
11．若集合A={x|x2-2x＜0}，B={x|y=lg（x-1）}，则A∩B（　　）
A．（0，1）B．（0，2）C．（1，2）D．（1，+∞）
8．曲线y=2x3与直线x=0，x=1及x轴所围成的平面的面积．
9．已知二次函数f（x）=x2+4x，三次函数g（x）=$\frac{1}{3}$bx3-bx2-3bx+1．
（1）探究；是否存在实数b，使得函数g（x）的图象经过四个象限，若存在，求实数b的取值范围；若不存在，请说明理由．
（2）若m，n是方程lnx-ax=0的两个不同的根，记函数h（x）=f（x）+g（x），当函数h（x）的图象在（0，h（0））处的切线平行于直线y=x+2时，求证：h（mn）＞h（e2）（e为自然对数底数）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网