题目内容
“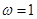 ”是“函数
”是“函数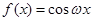 在区间
在区间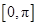 上单调递减”的( )
上单调递减”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
A
解析试题分析:P: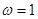 q:函数
q:函数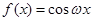 在区间
在区间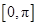 上单调递减 显然当
上单调递减 显然当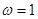 时,由余弦函数的图像可得函数
时,由余弦函数的图像可得函数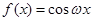 在区间
在区间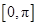 上单调递减,即
上单调递减,即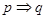 ,但是
,但是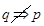 ,反例
,反例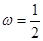 时, 函数
时, 函数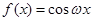 在区间
在区间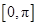 上也单调递减.所以“
上也单调递减.所以“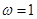 ”是“ 函数
”是“ 函数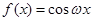 在区间
在区间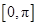 上单调递减”的充分不必要条件,故选A
上单调递减”的充分不必要条件,故选A
考点:余弦函数单调性 逻辑关系

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
在 中,
中, 是
是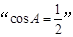 的( )
的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
下列命题正确的个数是 ( )
(1)命题“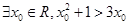 ”的否定是“
”的否定是“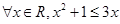 ”;
”;
(2)函数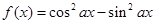 的最小正周期为
的最小正周期为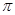 ”是“
”是“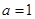 ”的必要不充分条件;
”的必要不充分条件;
(3)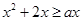 在
在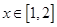 上恒成立
上恒成立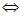
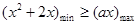 在
在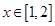 上恒成立
上恒成立
(4) “平面向量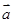 与
与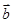 的夹角是钝角”的充分必要条件是“
的夹角是钝角”的充分必要条件是“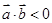 ”。
”。
| A.1 | B.2 | C.3 | D.4 |
已知命题p:?x∈R,2x<3x;命题q:?x∈R,x3=1-x2,则下列命题中为真命题的是( )
| A.p∧q | B.p∧q | C.p∧ q q | D.p∧ q q |
如果命题“ (p∨q)”是假命题,则下列说法正确的是( )
(p∨q)”是假命题,则下列说法正确的是( )
| A.p、q均为真命题 |
| B.p、q至少有一个为真命题 |
| C.p、q均为假命题 |
| D.p、q至少有一个为假命题 |
已知P:a>b>0,Q:a2>b2,那么P是Q成立的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
已知命题P:关于x的方程x2-ax+4=0有实根;命题Q:关于x的函数y=2x2+ax+4在[3,+∞)上是增函数.若P或Q是真命题,P且Q是假命题,则实数a的取值范围是( )
| A.(-12,-4]∪[4,+∞) |
| B.[-12,-4]∪[4,+∞) |
| C.(-∞,-12)∪(-4,4) |
| D.[-12,+∞) |
下列四个命题
p1:?x∈(0,+∞),( )x<(
)x<( )x;
)x;
p2:?x∈(0,1),lo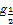 x>lo
x>lo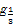 x;
x;
p3:?x∈(0, +∞),( )x>lo
)x>lo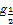 x;
x;
p4:?x∈(0, ),(
),( )x<lo
)x<lo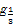 x.
x.
其中的真命题是( )
| A.p1,p3 | B.p1,p4 | C.p2,p3 | D.p2,p4 |
 ·
· =
=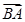 ·
· ,则|
,则|