题目内容
已知函数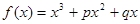 与
与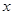 轴切于
轴切于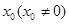 点,且极小值为
点,且极小值为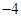 ,则
,则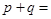 ( )
( )
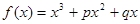 与
与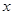 轴切于
轴切于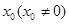 点,且极小值为
点,且极小值为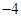 ,则
,则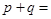 ( )
( )| A.12 | B.13 | C.15 | D.16 |
C
试题分析:根据题意由于函数
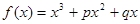 与
与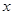 轴切于
轴切于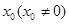 点,根据导数的几何意义可知,同时极小值为-4,那么可知有
点,根据导数的几何意义可知,同时极小值为-4,那么可知有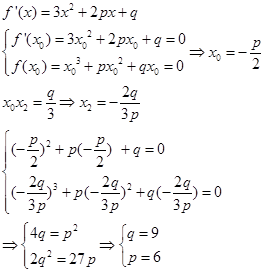
故可知p+q=15,选C.
点评:解决的关键是对于导数的几何意义的运用,以及极值的概念的综合运用,属于基础题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
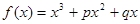 与
与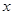 轴切于
轴切于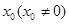 点,且极小值为
点,且极小值为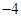 ,则
,则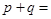 ( )
( )| A.12 | B.13 | C.15 | D.16 |
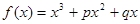 与
与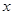 轴切于
轴切于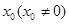 点,根据导数的几何意义可知,同时极小值为-4,那么可知有
点,根据导数的几何意义可知,同时极小值为-4,那么可知有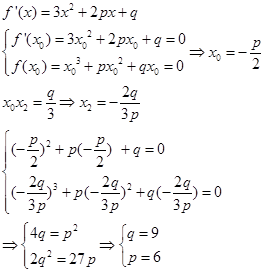

 名校课堂系列答案
名校课堂系列答案