题目内容
今有甲、乙两个篮球队进行比赛,比赛采用7局4胜制.假设甲、乙两队在每场比赛中获胜的概率都是| 1 | 2 |
(Ⅰ)求X大于5的概率;
(Ⅱ)求X的分布列与数学期望.
分析:(Ⅰ)依题意可知,X的可能取值最小为4.当X=4时,整个比赛只需比赛4场即结束,这意味着甲连胜4场,或乙连胜4场,可得X=4的概率;当X=5时,需要比赛5场整个比赛结束,意味着甲在第5场获胜,前4场中有3场获胜,或者乙在第5场获胜,前4场中有3场获胜.可得X=5的概率,从而得出X大于5的概率.
(II)由于X的可能取值为4,5,6,7,可得X的分布列,由公式即可得出篮球队在6场比赛中需要比赛的场数为X的期望.
(II)由于X的可能取值为4,5,6,7,可得X的分布列,由公式即可得出篮球队在6场比赛中需要比赛的场数为X的期望.
解答:解:(Ⅰ)依题意可知,X的可能取值最小为4.
当X=4时,整个比赛只需比赛4场即结束,这意味着甲连胜4场,或乙连胜4场,
可得P(X=4)=2×(
)4×(
)0=
.
当X=5时,需要比赛5场整个比赛结束,意味着甲在第5场获胜,前4场中有3场获胜,或者乙在第5场获胜,前4场中有3场获胜.
可得P(X=5)=2×[
×(
)3×
]×
=
.
所以P(X>5)=1-
-
=
.
(Ⅱ)X的可能取值为4,5,6,7,可得P(X=6)=2×[
×(
)3×(
)2]×
=
;P(X=7)=2×[
×(
)3×(
)3]×
=
.
所以X的分布列为:
X的数学期望为:EX=4×
+5×
+6×
+7×
=
.
当X=4时,整个比赛只需比赛4场即结束,这意味着甲连胜4场,或乙连胜4场,
可得P(X=4)=2×(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
当X=5时,需要比赛5场整个比赛结束,意味着甲在第5场获胜,前4场中有3场获胜,或者乙在第5场获胜,前4场中有3场获胜.
可得P(X=5)=2×[
| C | 3 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
所以P(X>5)=1-
| 1 |
| 8 |
| 1 |
| 4 |
| 5 |
| 8 |
(Ⅱ)X的可能取值为4,5,6,7,可得P(X=6)=2×[
| C | 3 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 16 |
| C | 3 6 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 16 |
所以X的分布列为:
| X | 4 | 5 | 6 | 7 | ||||||||
| P |
|
|
|
|
| 1 |
| 8 |
| 1 |
| 4 |
| 5 |
| 16 |
| 5 |
| 16 |
| 93 |
| 16 |
点评:本题考查二项分布与n次独立重复试验的模型,考查根据所给的事件类型选择概率模型的方法,以及用概率模型求概率与期望的能力.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
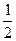 .并记需要比赛的场数为ξ.
.并记需要比赛的场数为ξ.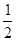 .并记需要比赛的场数为ξ.
.并记需要比赛的场数为ξ. .并记需要比赛的场数为X.
.并记需要比赛的场数为X.