题目内容
(14分)今有甲、乙两个篮球队进行比赛,比赛采用7局4胜制.假设甲、乙两队在每场比赛中获胜的概率都是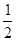 .并记需要比赛的场数为ξ.
.并记需要比赛的场数为ξ.
(Ⅰ)求ξ大于5的概率;(Ⅱ)求ξ的分布列与数学期望.
【答案】
.解:(Ⅰ)依题意可知,ξ的可能取值最小为4.
当ξ=4时,整个比赛只需比赛4场即结束,这意味着甲连胜4场,或乙连胜4场,于是,由互斥事件的概率计算公式,可得
P(ξ=4)=2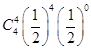 =
=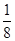 .……………..2分
.……………..2分
当ξ=5时,需要比赛5场整个比赛结束,意味着甲在第5场获胜,前4场中有3场获胜,或者乙在第5场获胜,前4场中有3场获胜.显然这两种情况是互斥的,于是,
P(ξ=5)=2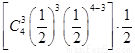 =
=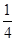 ,…………….4分
,…………….4分
∴P(ξ>5)=1-[P(ξ=4)+P(ξ=5)]=1-[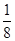 +
+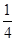 ]=
]=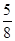 .…………….6分
.…………….6分
即ξ>5的概率为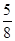 .
.
(Ⅱ)∵ξ的可能取值为4,5,6,7,仿照(Ⅰ),可得
P (ξ=6)=2
(ξ=6)=2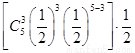 =
=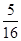 ,………………..8分
,………………..8分
P(ξ=7)=2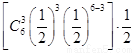 =
=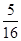 ,………………..10分
,………………..10分
∴ξ的分布列为:
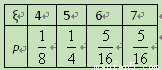 ………………………………………………………
……………………………………………………… ..12分[
..12分[
ξ的数学期望为:Eξ=4·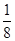 +5·
+5·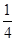 +6·
+6·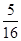 +7·
+7·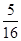
 =
=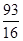 .……………14分
.……………14分
【解析】略

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
 .并记需要比赛的场数为ξ.
.并记需要比赛的场数为ξ. .并记需要比赛的场数为X.
.并记需要比赛的场数为X.