题目内容
已知椭圆C: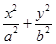 =1(a>b>0)的离心率与等轴双曲线的离心率互为倒数关系,直线l:x-y+
=1(a>b>0)的离心率与等轴双曲线的离心率互为倒数关系,直线l:x-y+ =0与以原点为圆心, 以椭圆C的短半轴长为半径的圆相切.
=0与以原点为圆心, 以椭圆C的短半轴长为半径的圆相切.
(1)求椭圆C的方程;
(2)设M是椭圆的上顶点,过点M分别作直线MA,MB交椭圆于A,B两点,设两直线的斜率分别为k1,k2,且k1+k2=4,证明:直线AB过定点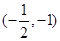 .
.
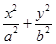 =1(a>b>0)的离心率与等轴双曲线的离心率互为倒数关系,直线l:x-y+
=1(a>b>0)的离心率与等轴双曲线的离心率互为倒数关系,直线l:x-y+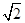 =0与以原点为圆心, 以椭圆C的短半轴长为半径的圆相切.
=0与以原点为圆心, 以椭圆C的短半轴长为半径的圆相切.(1)求椭圆C的方程;
(2)设M是椭圆的上顶点,过点M分别作直线MA,MB交椭圆于A,B两点,设两直线的斜率分别为k1,k2,且k1+k2=4,证明:直线AB过定点
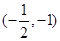 .
.(1) +y2=1.(2)见解析
+y2=1.(2)见解析
 +y2=1.(2)见解析
+y2=1.(2)见解析(1)∵等轴双曲线离心率为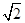 ,∴椭圆C的离心率e=
,∴椭圆C的离心率e= .
.
∴e2= =
= ,∴a2=2b2.
,∴a2=2b2.
∵由x-y+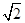 =0与圆x2+y2=b2相切,得
=0与圆x2+y2=b2相切,得
b=1,∴a2=2.
∴椭圆C的方程为 +y2=1.
+y2=1.
(2)证明 ①若直线AB的斜率不存在,设方程为x=x0,则点A(x0,y0),B(x0,-y0).
由已知 =4,得x0=-
=4,得x0=- .
.
此时AB方程为x=- ,显然过点
,显然过点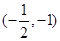 .
.
②若直线AB的斜率存在,设AB方程为y=kx+m,依题意m≠±1.
设A(x1,y1),B(x2,y2),由
得(1+2k2)x2+4kmx+2m2-2=0.
则x1+x2=- ,x1x2=
,x1x2= .
.
由已知k1+k2=4,可得 +
+ =4,
=4,
∴ +
+ =4,即2k+(m-1)
=4,即2k+(m-1)  =4,将x1+x2,x1x2代入得k-
=4,将x1+x2,x1x2代入得k- =2,∴k=2(m+1),
=2,∴k=2(m+1),
∴m= -1.故直线AB的方程为y=kx+
-1.故直线AB的方程为y=kx+ -1,
-1,
即y=k -1.
-1.
∴直线AB过定点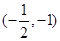 .
.
综上,直线AB过定点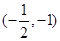 .
.
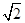 ,∴椭圆C的离心率e=
,∴椭圆C的离心率e= .
.∴e2=
 =
= ,∴a2=2b2.
,∴a2=2b2.∵由x-y+
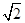 =0与圆x2+y2=b2相切,得
=0与圆x2+y2=b2相切,得b=1,∴a2=2.
∴椭圆C的方程为
 +y2=1.
+y2=1.(2)证明 ①若直线AB的斜率不存在,设方程为x=x0,则点A(x0,y0),B(x0,-y0).
由已知
 =4,得x0=-
=4,得x0=- .
.此时AB方程为x=-
 ,显然过点
,显然过点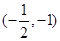 .
.②若直线AB的斜率存在,设AB方程为y=kx+m,依题意m≠±1.
设A(x1,y1),B(x2,y2),由

得(1+2k2)x2+4kmx+2m2-2=0.
则x1+x2=-
 ,x1x2=
,x1x2= .
.由已知k1+k2=4,可得
 +
+ =4,
=4,∴
 +
+ =4,即2k+(m-1)
=4,即2k+(m-1)  =4,将x1+x2,x1x2代入得k-
=4,将x1+x2,x1x2代入得k- =2,∴k=2(m+1),
=2,∴k=2(m+1),∴m=
 -1.故直线AB的方程为y=kx+
-1.故直线AB的方程为y=kx+ -1,
-1,即y=k
 -1.
-1.∴直线AB过定点
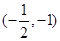 .
.综上,直线AB过定点
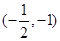 .
.
练习册系列答案
相关题目
 的焦点为
的焦点为 ,点
,点 ,线段
,线段 的中点在抛物线上. 设动直线
的中点在抛物线上. 设动直线 与抛物线相切于点
与抛物线相切于点 ,且与抛物线的准线相交于点
,且与抛物线的准线相交于点 ,以
,以 为直径的圆记为圆
为直径的圆记为圆 .
. 的值;
的值; 轴必有公共点;
轴必有公共点; ,使得圆
,使得圆 与
与 的离心率相等. 直线
的离心率相等. 直线 与曲线
与曲线 交于
交于 两点(
两点( 在
在 的左侧),与曲线
的左侧),与曲线 交于
交于 两点(
两点( 在
在 的左侧),
的左侧), 为坐标原点,
为坐标原点, .
. =
= ,
, 时,求椭圆
时,求椭圆 的方程;
的方程; ,且
,且 和
和 相似,求
相似,求
 过点
过点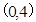 ,离心率为
,离心率为 .
. 的方程;
的方程; 且斜率为
且斜率为 的直线被椭圆所截得线段的中点坐标.
的直线被椭圆所截得线段的中点坐标. :
: ,直线
,直线 交椭圆
交椭圆 两点.
两点. 为直径的圆的方程.
为直径的圆的方程.  =1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径.l1,l2是过点P且互相垂直的两条直线,其中l1交圆C2于A,B两点,l2交椭圆C1于另一点D.
=1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径.l1,l2是过点P且互相垂直的两条直线,其中l1交圆C2于A,B两点,l2交椭圆C1于另一点D.
 轴上,焦距为2,直线n:x-y-1=0与椭圆C交于A、B两点,F1是左焦点,且
轴上,焦距为2,直线n:x-y-1=0与椭圆C交于A、B两点,F1是左焦点,且 ,则椭圆C的标准方程是
,则椭圆C的标准方程是  左焦点
左焦点 且倾斜角为
且倾斜角为 的直线交双曲线右支于点
的直线交双曲线右支于点 ,若线段
,若线段 的中点
的中点 落在
落在 轴上,则此双曲线的离心率为( )
轴上,则此双曲线的离心率为( )



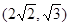 的双曲线
的双曲线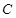 的渐近线方程为
的渐近线方程为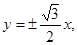
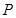 为双曲线
为双曲线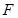 为双曲线
为双曲线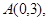 则
则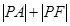 的最小值为 .
的最小值为 .