题目内容
7.将函数y=sin$\frac{x}{2}$的图象按向量$\overrightarrow{a}$平移后,得到y=cos($\frac{x}{2}$-$\frac{π}{4}$)的图象,则向量$\overrightarrow{a}$的坐标可能为( )| A. | ($\frac{π}{2}$,0) | B. | (-$\frac{π}{2}$,0) | C. | ($\frac{π}{4}$,0) | D. | (-$\frac{π}{4}$,0) |
分析 由条件根据函数y=Asin(ωx+φ)的图象变换规律,可得结论.
解答 解:函数y=sin$\frac{x}{2}$的图象按向量$\overrightarrow{a}$平移后,得到y=cos($\frac{x}{2}$-$\frac{π}{4}$)的图象,
而把函数y=sin$\frac{x}{2}$的图象项由平移$\frac{π}{2}$个单位,得到y=cos$\frac{1}{2}$(x-$\frac{π}{2}$)=cos($\frac{x}{2}$-$\frac{π}{4}$)的图象
则向量$\overrightarrow{a}$的坐标可能是($\frac{π}{2}$,0),
故选:A.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
相关题目
18.tan$\frac{π}{8}$-$\frac{1}{tan\frac{π}{8}}$的值是( )
| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
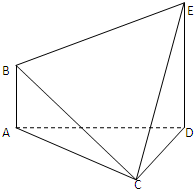 在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1.
在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1. 如图,在五面体P-ABCD中,CB⊥平面ABP,BC∥AD,AD=2BC=2,且BA=BP=2,BA⊥BP.
如图,在五面体P-ABCD中,CB⊥平面ABP,BC∥AD,AD=2BC=2,且BA=BP=2,BA⊥BP.