题目内容
在 中,已知
中,已知
 ,面积
,面积 ,
,
(1)求 的三边的长;
的三边的长;
(2)设 是
是 (含边界)内的一点,
(含边界)内的一点, 到三边
到三边 的距离分别是
的距离分别是
①写出 所满足的等量关系;
所满足的等量关系;
②利用线性规划相关知识求出 的取值范围.
的取值范围.
 中,已知
中,已知
 ,面积
,面积 ,
,(1)求
 的三边的长;
的三边的长;(2)设
 是
是 (含边界)内的一点,
(含边界)内的一点, 到三边
到三边 的距离分别是
的距离分别是
①写出
 所满足的等量关系;
所满足的等量关系;②利用线性规划相关知识求出
 的取值范围.
的取值范围.(1)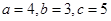 (2)
(2)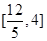
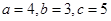 (2)
(2)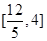
第一问中利用设 中角
中角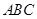 所对边分别为
所对边分别为
由 得
得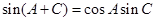
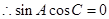
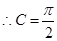
又由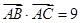 得
得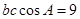 即
即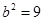
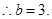
又由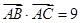 得
得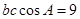 即
即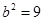
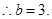
又
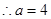 又
又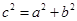 得
得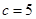
即 的三边长
的三边长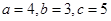

第二问中,①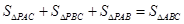 得
得
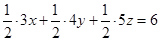
故
②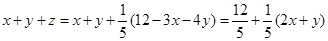
令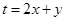 依题意有
依题意有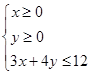
作图,然后结合区域得到最值。

 中角
中角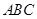 所对边分别为
所对边分别为
由
 得
得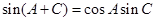
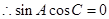
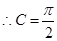
又由
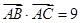 得
得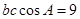 即
即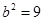
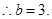
又由
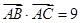 得
得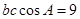 即
即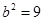
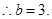
又

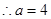 又
又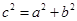 得
得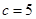
即
 的三边长
的三边长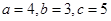

第二问中,①
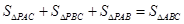 得
得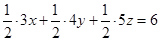
故

②
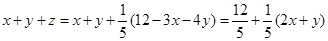
令
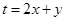 依题意有
依题意有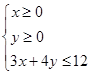
作图,然后结合区域得到最值。


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
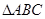 中,
中,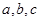 分别为
分别为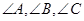 的对边,已知
的对边,已知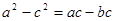 .
.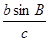 的值.
的值. 中,内角
中,内角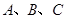 的对边的边长为
的对边的边长为 ,且
,且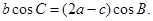
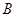 的大小;
的大小;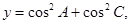 求
求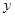 的取值范围.
的取值范围. 是椭圆
是椭圆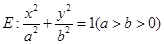 的左、右焦点,
的左、右焦点, 为直线
为直线 上一点,
上一点, 是底角为
是底角为 的等腰三角形,则
的等腰三角形,则 的离心率为( )
的离心率为( )



 ,
, ,于水面C处测得B点和D点的仰角均为
,于水面C处测得B点和D点的仰角均为 ,AC=0.1km。则B,D间距离为_______________km.
,AC=0.1km。则B,D间距离为_______________km. 
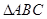 中,角
中,角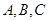 所对的边分别是
所对的边分别是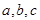 ,且
,且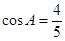 .
.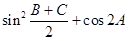 的值;
的值;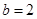 ,
,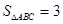 ,求边
,求边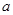 .
. 中,内角A、B、C所对边的长分别是a、b、c,且点
中,内角A、B、C所对边的长分别是a、b、c,且点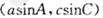 在直线
在直线 上.
上.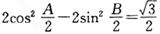 ,且A<B,求.
,且A<B,求. 的值.
的值.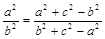 ,则△ABC是( )
,则△ABC是( )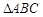 的三内角满足:
的三内角满足: 且
且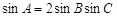 ,则
,则