题目内容
已知 ,不等式
,不等式 的解集为
的解集为 .
.
(1)求 的值;
的值;
(2)若 对一切实数
对一切实数 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(1)2;(2)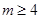 .
.
解析试题分析:(1)我们首先求出不等式 的解集,这个解集与
的解集,这个解集与 相等,由此可求得
相等,由此可求得 ;(2)
;(2) ,一种方法,这个函数是分段函数,我们把它化为一般的分段函数表达式,以便求出它的最大(小)值,从而求得
,一种方法,这个函数是分段函数,我们把它化为一般的分段函数表达式,以便求出它的最大(小)值,从而求得 的最大值,得到
的最大值,得到 的取值范围,也可应用绝对值不等式的性质
的取值范围,也可应用绝对值不等式的性质 ,求得最大值.
,求得最大值.
试题解析:解法一:(1)由不等式|2x-a|-a≤2,得|2x-a|≤2+a,
∵解集不空,∴2+a≥0.
解不等式可得{x∣-1≤x≤1+a}. 3分
∵-1≤x≤3,∴1+a﹦3,即a=2. 5分
(2)记g(x)=f(x)-f(x+2)=|2x-2|-|2x+2|, 6分
4,(x≤-1)
则g(x)=-4x,(-1﹤x﹤1). 8分
-4,(x≥1)
所以-4≤g(x)≤4,∴|g(x)|≤4,因此m≥4. 10分
解法二:∵f(x)-f(x+2)=|2x-2|-|2x+2|,
∵|2x-2|-|2x+2|≤|(2x-2)-(2x+2)|=4. 7分
|2x-2|-|2x+2|≥|2x|-2-(|2x|+2)=-4. 9分
∴-4≤|2x-2|-|2x+2|≤4.
∴|f(x)-f(x+2)|≤4.
∴m≥4. 10分
考点:(1)解绝对值不等式;(2)分段函数的最值,不等式恒成立问题.

练习册系列答案
相关题目
 是二次函数,不等式
是二次函数,不等式 的解集是(0,5),且
的解集是(0,5),且 在区间
在区间 内有且只有两个不等的实数根?若存在,求出所有m的值;若不存在,请说明理由.
内有且只有两个不等的实数根?若存在,求出所有m的值;若不存在,请说明理由. .
. 在
在 上的最大值和最小值;
上的最大值和最小值; 时,函数
时,函数 的下方.
的下方. ,若存在非零常数
,若存在非零常数 ,使函数
,使函数 ,都有
,都有 ,则称函数
,则称函数 为函数
为函数 称为周距.
称为周距. 是以2为广义周期的广义周期函数,并求出它的相应周距
是以2为广义周期的广义周期函数,并求出它的相应周距 ,使
,使 (
( 为常数,
为常数, )为广义周期函数,并求出它的一个广义周期
)为广义周期函数,并求出它的一个广义周期 的周期函数,当函数
的周期函数,当函数 在
在 上的值域为
上的值域为 时,求
时,求 上的最大值和最小值.
上的最大值和最小值.
 的单调性;
的单调性; 时,关于
时,关于 的方程
的方程 有唯一解,求
有唯一解,求 的值;
的值; 时,证明: 对一切
时,证明: 对一切 ,都有
,都有 成立.
成立. (
( 为参数),以原点为极点,x轴的正半轴为极轴,并取与直角坐标系相同的长度单位,建立极坐标系,曲线C2是极坐标方程为:
为参数),以原点为极点,x轴的正半轴为极轴,并取与直角坐标系相同的长度单位,建立极坐标系,曲线C2是极坐标方程为: ,
, 的最小值.
的最小值. .
. ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程; 的图象在区间
的图象在区间 上有公共点,求实数
上有公共点,求实数 的取值范围.
的取值范围. 图象;
图象;