题目内容
定义:对于函数 ,若存在非零常数
,若存在非零常数 ,使函数
,使函数 对于定义域内的任意实数
对于定义域内的任意实数 ,都有
,都有 ,则称函数
,则称函数 是广义周期函数,其中称
是广义周期函数,其中称 为函数
为函数 的广义周期,
的广义周期, 称为周距.
称为周距.
(1)证明函数 是以2为广义周期的广义周期函数,并求出它的相应周距
是以2为广义周期的广义周期函数,并求出它的相应周距 的值;
的值;
(2)试求一个函数 ,使
,使 (
( 为常数,
为常数, )为广义周期函数,并求出它的一个广义周期
)为广义周期函数,并求出它的一个广义周期 和周距
和周距 ;
;
(3)设函数 是周期
是周期 的周期函数,当函数
的周期函数,当函数 在
在 上的值域为
上的值域为 时,求
时,求 在
在 上的最大值和最小值.
上的最大值和最小值.
(1)2;(2)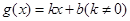 ,
,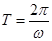 ,
,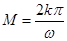 ;(3)
;(3)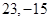 .
.
解析试题分析:本题是一个新定义概念问题,解决问题的关键是按照新定义把问题转化为我们熟悉的问题,(1)就是找到 使
使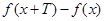
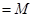 为常数,考虑到
为常数,考虑到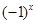
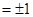 ,因此取
,因此取 ,则有
,则有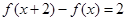 ,符合题设,即得
,符合题设,即得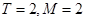 ;(2)在(1)中求解时,可以想到一次函数就是广义周期函数,因此取
;(2)在(1)中求解时,可以想到一次函数就是广义周期函数,因此取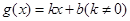 ,再考虑到正弦函数的周期性,取
,再考虑到正弦函数的周期性,取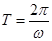 ,代入新定义式子
,代入新定义式子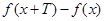 计算可得;(3)首先,函数
计算可得;(3)首先,函数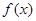 应该是广义周期函数,由新定义可求得一个广义周期是
应该是广义周期函数,由新定义可求得一个广义周期是 ,周距
,周距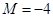 ,由于
,由于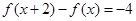
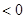 ,可见
,可见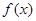 在区间
在区间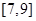 上取得最小值,在
上取得最小值,在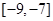 上取得最大值,而当
上取得最大值,而当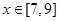 时,由上面结论可得
时,由上面结论可得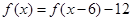
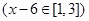 ,最小值为
,最小值为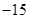 ,当
,当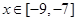 时,
时,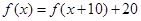 ,从而最大值为
,从而最大值为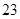 .
.
试题解析:(1)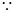
 ,
,
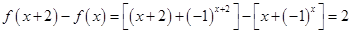 ,(非零常数)
,(非零常数)
所以函数 是广义周期函数,它的周距为2. (4分)
是广义周期函数,它的周距为2. (4分)
(2)设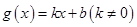 ,则
,则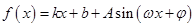
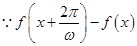
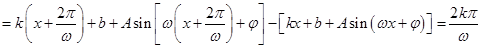
(非零常数) 所以 是广义周期函数,且
是广义周期函数,且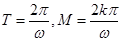 . ( 9分)
. ( 9分)
(3)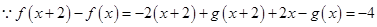 ,
,
所以 是广义周期函数,且
是广义周期函数,且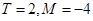 . (10分)
. (10分)
设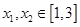 满足
满足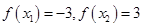 ,
,
由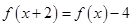 得:
得: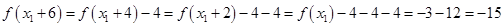 ,
,
又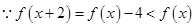 知道
知道 在区间
在区间 上的最小值是
上的最小值是 在
在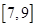 上获得的,而
上获得的,而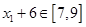 ,所以
,所以 在
在 上的最小值为
上的最小值为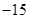 . ( 13分)
. ( 13分)
由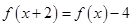 得
得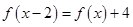 得:
得: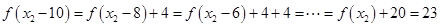 ,
,
又 知道
知道 在区间
在区间 上的最大值是
上的最大值是 在
在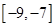 上获得的,
上获得的,
而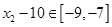 ,所以
,所以

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目

 .
. 的奇偶性;
的奇偶性; 上为减函数,求
上为减函数,求 的取值范围.
的取值范围.
 的图象切x轴于点(2,0),求a、b的值;
的图象切x轴于点(2,0),求a、b的值;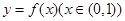 的图象上任意一点的切线斜率为k,试求
的图象上任意一点的切线斜率为k,试求 的充要条件;
的充要条件; .
. 在
在 上为增函数,则称
上为增函数,则称 为“k次比增函数”,其中
为“k次比增函数”,其中 . 已知
. 已知 其中e为自然对数的底数.
其中e为自然对数的底数. 时,求函数
时,求函数 在
在 上的最小值;
上的最小值; .
. 是实数,函数
是实数,函数 (
( ).
). 不是奇函数;
不是奇函数; 时,求满足
时,求满足 的
的 的取值范围;
的取值范围; 的值域(用
的值域(用 ,
, .
. ,求证:函数
,求证:函数 是
是 上的奇函数;
上的奇函数; 上没有零点,求实数
上没有零点,求实数 的取值范围.
的取值范围. ,不等式
,不等式 的解集为
的解集为 .
. 的值;
的值; 对一切实数
对一切实数 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.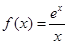 的定义域为
的定义域为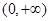 .
. 在
在 上的最小值;
上的最小值; ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. .
.