题目内容
若n∈Z,在①sin(nπ+
),②sin(2nπ±
),③sin[nπ+(-1)n
)],④cos[2nπ+(-1)n
]中,与sin
相等的是( )
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| A、①和② | B、③和④ |
| C、①和④ | D、②和③ |
分析:分别求出①②③④四个表达式的值,等于
的即可满足要求.
| ||
| 2 |
解答:解:①sin(nπ+
)=±sin
=±
,
②sin(2nπ±
)=±sin
=±
;
③sin[nπ+(-1)n
)]=sin
=
cos[2nπ+(-1)n
]=cos
=
所以③④满足题意,
故选B
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
②sin(2nπ±
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
③sin[nπ+(-1)n
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
cos[2nπ+(-1)n
| π |
| 6 |
| π |
| 6 |
| ||
| 2 |
所以③④满足题意,
故选B
点评:本题是基础题,考查三角函数的化简求值,诱导公式的应用,考查计算能力,常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
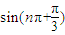 ,②
,②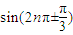 ,③
,③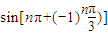 ,④
,④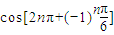 中,与sin
中,与sin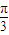 相等的是( )
相等的是( )