题目内容
(1)若点A(a,b)(其中a≠b)在矩阵M=
对应变换的作用下得到的点为B(-b,a).
(Ⅰ)求矩阵M的逆矩阵;
(Ⅱ)求曲线C:x2+y2=1在矩阵N=
所对应变换的作用下得到的新的曲线C′的方程.
(2)选修4-4:坐标系与参数方程
(Ⅰ)以直角坐标系的原点为极点,x轴的正半轴为极轴,并在两种坐标系中取相同的长度单位已知直线的极坐标方程为θ=
(ρ∈R),它与曲线
(θ为参数)相交于两点A和B,求|AB|;
(Ⅱ)已知极点与原点重合,极轴与x轴正半轴重合,若直线C1的极坐标方程为:ρcos(θ-
)=
,曲线C2的参数方程为:
(θ为参数),试求曲线C2关于直线C1对称的曲线的直角坐标方程.
(3)选修4-5:不等式选讲
(Ⅰ)已知函数f(x)=|x+3|,g(x)=m-2|x-11|,若2f(x)≥g(x+4)恒成立,求实数m的取值范围.
(Ⅱ)已知实数x、y、z满足2x2+3y2+6z2=a(a>0),且x+y+z的最大值是1,求a的值.
|
(Ⅰ)求矩阵M的逆矩阵;
(Ⅱ)求曲线C:x2+y2=1在矩阵N=
|
(2)选修4-4:坐标系与参数方程
(Ⅰ)以直角坐标系的原点为极点,x轴的正半轴为极轴,并在两种坐标系中取相同的长度单位已知直线的极坐标方程为θ=
| π |
| 4 |
|
(Ⅱ)已知极点与原点重合,极轴与x轴正半轴重合,若直线C1的极坐标方程为:ρcos(θ-
| π |
| 4 |
| 2 |
|
(3)选修4-5:不等式选讲
(Ⅰ)已知函数f(x)=|x+3|,g(x)=m-2|x-11|,若2f(x)≥g(x+4)恒成立,求实数m的取值范围.
(Ⅱ)已知实数x、y、z满足2x2+3y2+6z2=a(a>0),且x+y+z的最大值是1,求a的值.
分析:(1)(Ⅰ)求出矩阵的行列式,从而可得矩阵M的逆矩阵;
(Ⅱ)设(x′,y′)在矩阵N=
所对应变换的作用下的点为(x,y),从而可得坐标之间的关系,代入x2+y2=1,即可得结论;
(2)(Ⅰ)求出直线和圆的直角坐标方程、圆心到直线y=x的距离,利用垂径定理,可得结论;
(Ⅱ)求出直线C1的直角坐标方程;曲线C2的普通方程,从而可求曲线C2关于直线C1对称的曲线的直角坐标方程;
(3)(Ⅰ)条件可转化为m≤2(|x-7|+|x+3|),由绝对值不等式的性质可得实数m的取值范围;
(Ⅱ)由柯西不等式可得[(
x)2+(
y)2+(
z)2][(
)2+(
)2+(
)2]≥x+y+z,由此可得结论.
(Ⅱ)设(x′,y′)在矩阵N=
|
(2)(Ⅰ)求出直线和圆的直角坐标方程、圆心到直线y=x的距离,利用垂径定理,可得结论;
(Ⅱ)求出直线C1的直角坐标方程;曲线C2的普通方程,从而可求曲线C2关于直线C1对称的曲线的直角坐标方程;
(3)(Ⅰ)条件可转化为m≤2(|x-7|+|x+3|),由绝对值不等式的性质可得实数m的取值范围;
(Ⅱ)由柯西不等式可得[(
| 2 |
| 3 |
| 6 |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
解答:解:(1)(Ⅰ)∵矩阵M=
,∴矩阵的行列式为
=1≠0
∴M-1=
;
(Ⅱ)设(x′,y′)在矩阵N=
所对应变换的作用下的点为(x,y),则
=
,∴
代入x2+y2=1,可得4x2+y2=1;
(2)(Ⅰ)直线和圆的直角坐标方程分别为y=x和(x-1)2+(y-2)2=5,则圆心为C(1,2),半径R=
从而C到直线y=x的距离d=
=
由垂径定理得|AB|=2
=3
(Ⅱ)直线C1的极坐标方程为:ρcos(θ-
)=
,直角坐标方程为x+y=2;曲线C2的参数方程为:
(θ为参数),普通方程为:(x-1)2+(y-3)2=1,圆心坐标为(1,3),半径为1
圆心坐标为(1,3)关于x+y=2对称点的坐标为(1,-1),
∴曲线C2关于直线C1对称的曲线的直角坐标方程为(x+1)2+(y-1)2=1;
(3)(Ⅰ)已知函数f(x)=|x+3|,g(x)=m-2|x-11|,若2f(x)≥g(x+4)恒成立,即m≤2(|x-7|+|x+3|)
由绝对值不等式的性质可得2(|x-7|+|x+3|)≥2|x-7-(x+3)|=20
∴实数m的取值范围为(-∞,20];
(Ⅱ)由柯西不等式可得[(
x)2+(
y)2+(
z)2][(
)2+(
)2+(
)2]≥x+y+z
∵2x2+3y2+6z2=a(a>0),∴a≥(x+y+z)2,
∵x+y+z的最大值是1,∴a=1,
当2x=3y=6z时,x+y+z取最大值,∴a=1.
|
|
∴M-1=
|
(Ⅱ)设(x′,y′)在矩阵N=
|
|
|
|
|
代入x2+y2=1,可得4x2+y2=1;
(2)(Ⅰ)直线和圆的直角坐标方程分别为y=x和(x-1)2+(y-2)2=5,则圆心为C(1,2),半径R=
| 5 |
从而C到直线y=x的距离d=
| |1-2| | ||
|
| ||
| 2 |
由垂径定理得|AB|=2
| R2-d2 |
| 2 |
(Ⅱ)直线C1的极坐标方程为:ρcos(θ-
| π |
| 4 |
| 2 |
|
圆心坐标为(1,3)关于x+y=2对称点的坐标为(1,-1),
∴曲线C2关于直线C1对称的曲线的直角坐标方程为(x+1)2+(y-1)2=1;
(3)(Ⅰ)已知函数f(x)=|x+3|,g(x)=m-2|x-11|,若2f(x)≥g(x+4)恒成立,即m≤2(|x-7|+|x+3|)
由绝对值不等式的性质可得2(|x-7|+|x+3|)≥2|x-7-(x+3)|=20
∴实数m的取值范围为(-∞,20];
(Ⅱ)由柯西不等式可得[(
| 2 |
| 3 |
| 6 |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
∵2x2+3y2+6z2=a(a>0),∴a≥(x+y+z)2,
∵x+y+z的最大值是1,∴a=1,
当2x=3y=6z时,x+y+z取最大值,∴a=1.
点评:本题考查选修知识,考查矩阵与变换,考查坐标系与参数方程,考查不等式选讲,综合性强.

练习册系列答案
相关题目
若点A(a,0),B(0,b),C(1,-1)(a>0,b<0)三点共线,则a-b的最小值等于( )
| A、4 | B、2 | C、1 | D、0 |
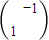 对应变换的作用下得到的点为B(-b,a).
对应变换的作用下得到的点为B(-b,a).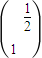 所对应变换的作用下得到的新的曲线C′的方程.
所对应变换的作用下得到的新的曲线C′的方程.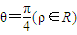 ,它与曲线
,它与曲线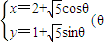 为参数)相交于两点A和B,求|AB|;
为参数)相交于两点A和B,求|AB|;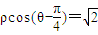 ,曲线C2的参数方程为:
,曲线C2的参数方程为: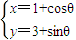 (θ为参数),试求曲线C2关于直线C1对称的曲线的直角坐标方程.
(θ为参数),试求曲线C2关于直线C1对称的曲线的直角坐标方程.