题目内容
在△OAB中,(1)用a、b表示![]() .
.
(2)在已知线段![]() 上取一点E,在线段
上取一点E,在线段![]() 上取一点F,使
上取一点F,使![]() 过点M.设
过点M.设![]() =p
=p![]() ,
,![]() =q
=q![]() ,求证:
,求证:![]()
(1)解析:设![]() =ma+nb,则
=ma+nb,则![]() =
=![]() -
-![]() =ma+nb-a=(m-1)a+nb,
=ma+nb-a=(m-1)a+nb,
![]() =
=![]() -
-![]() =
=![]() b-a=-a+
b-a=-a+![]() b.
b.
∵A、M、D三点共线,∴![]() 与
与![]() 共线.
共线.
∴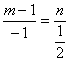 .∴m+2n=1.①
.∴m+2n=1.①
而![]() =
=![]() -
-![]()
=ma+nb-![]() a=(m-
a=(m-![]() )a+nb,
)a+nb,
![]() =
=![]() -
-![]() =b-
=b-![]() a=-
a=-![]() a+b,
a+b,
又∵C、M、B三点共线,∴![]() 与
与![]() 共线.
共线.
∴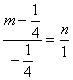 .∴4m+n=1.②
.∴4m+n=1.②
∴联立①②解得m=![]() ,n=
,n=![]() .
.
∴![]() =
=![]() a+
a+![]() b.
b.
(2)证明:∵![]() =
=![]() -
-![]() =
=![]() a+
a+![]() b-p
b-p![]() =
=![]() a+
a+![]() b-pa=(
b-pa=(![]() -p)a+
-p)a+![]() b,
b,
![]() =
=![]() -
-![]() =q
=q![]() -p
-p![]() =qb-pa=-pa+qb,
=qb-pa=-pa+qb,
又∵![]() 与
与![]() 共线,∴
共线,∴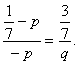
∴![]() q-pq=-
q-pq=-![]() p.∴
p.∴![]() p+
p+![]() q=1.
q=1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
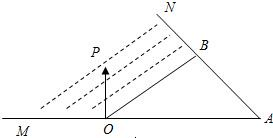 如图,在△OAB中,点P是线段OB及AB、AO的延长线所围成的阴影区域内(含边界)的任意一点,且
如图,在△OAB中,点P是线段OB及AB、AO的延长线所围成的阴影区域内(含边界)的任意一点,且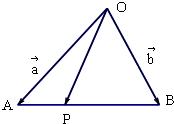 在△OAB中,点P在边AB上,
在△OAB中,点P在边AB上,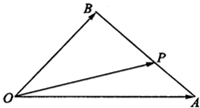 如图,在△OAB中,已知P为线段AB上的一点,若
如图,在△OAB中,已知P为线段AB上的一点,若