Question

（09年东城区期末文）(14分)

已知点N)都在函数的图象上.

(Ⅰ)若数列是等差数列,求证数列为等比数列；

(Ⅱ)若数列的前项和为=,过点的直线与两坐标轴所围成三角

    形面积为,求使对N恒成立的实数的取值范围.

Answer 1

解析：(Ⅰ)因为数列是等差数列,故设公差为,

则对N恒成立.依题意

,.

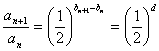由,所以是定值,

从而数列是等比数列.                                 …………5分

(Ⅱ)当时,,当时,,

当时也适合此式,即数列的通项公式是.                         …………7分

由,数列的通项公式是.                  ……………8分

   所以,过这两点的直线方程是,该直线与坐标轴的交点是和.

.                        ……………11分

因为.

即数列的各项依次单调递减,所以要使对N恒成立,只要,又,可得的取值范围是.                   …………13分

故实数的取值范围是.                          …………14分