题目内容
1.已知数列{an},a1=1,$\frac{{a}_{n}}{{a}_{n-1}}$=3n-1(n≥2,n∈N*).(1)求数列{an}的通项公式;
(2)若数列{bn}的前n项和Sn=log3($\frac{{a}_{n}}{2{7}^{3n}}$),求数列{bn}的通项公式;
(3)求数列{|bn|}的前n项和Tn.
分析 (1)由已知直接利用累积法求得数列{an}的通项公式;
(2)把数列{an}的通项公式代入Sn=log3($\frac{{a}_{n}}{2{7}^{3n}}$),利用对数的运算性质整理得到数列{bn}的前n项和Sn,
求出数列首项,再由bn=Sn-Sn-1求得数列通项公式;
(3)由数列{bn}得通项公式得到数列是以-9为首项,以1为公差的等差数列,bn=n-10≤0,得n≤10,说明数列{bn}的前10项小于等于0,自第11项起大于0,
然后分n≤10和n>10求得数列{|bn|}的前n项和Tn.
解答 解:(1)由a1=1,$\frac{{a}_{n}}{{a}_{n-1}}$=3n-1(n≥2,n∈N*),得
${a}_{n}=\frac{{a}_{n}}{{a}_{n-1}}•\frac{{a}_{n-1}}{{a}_{n-2}}…\frac{{a}_{2}}{{a}_{1}}•{a}_{1}$=3n-1•3n-2…31•1=31+2+…+(n-1)=${3}^{\frac{(n-1)n}{2}}$(n≥2,n∈N*).
当n=1时,上式成立,
∴${a}_{n}={3}^{\frac{(n-1)n}{2}}$;
(2)由Sn=log3($\frac{{a}_{n}}{2{7}^{3n}}$)=$lo{g}_{3}(\frac{{3}^{\frac{(n-1)n}{2}}}{2{7}^{3n}})$=$lo{g}_{3}{3}^{\frac{{n}^{2}-19n}{2}}$=$\frac{{n}^{2}-19n}{2}$.
当n=1时,b1=S1=-9;
当n≥2时,bn=Sn-Sn-1=$\frac{{n}^{2}-19n}{2}-\frac{(n-1)^{2}-19(n-1)}{2}$=n-10.
当n=1时上式成立.
∴bn=n-10;
(3)∵bn=n-10,∴bn+1-bn=1,
则数列{bn}是以-9为首项,以1为公差的等差数列,
由bn=n-10≤0,得n≤10,
∴数列{bn}的前10项小于等于0,自第11项起大于0,
当n≤10时,Tn=|b1|+|b2|+…+|bn|=-(b1+b2+…+bn)=-[-9n+$\frac{n(n-1)×1}{2}$]=$-\frac{{n}^{2}-19n}{2}$;
当n>10时,Tn=|b1|+|b2|+…+|bn|=-(b1+b2+…+b10)+(b11+…+bn)
=-2(b1+b2+…+b10)+(b1+b2+…+b10+b11+…+bn)
=-2×$\frac{1{0}^{2}-190}{2}$+$\frac{{n}^{2}-19n}{2}$=$\frac{{n}^{2}-19n+180}{2}$.
∴${T}_{n}=\left\{\begin{array}{l}{-\frac{{n}^{2}-19n}{2},n≤10}\\{\frac{{n}^{2}-19n+180}{2},n>10}\end{array}\right.$.
点评 本题考查了数列递推式,考查了累积法求数列的通项公式,考查了等差数列的前n项和,是中档题.

 如图,在多面体ABCDEF中,矩形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点,N为CD的中点.
如图,在多面体ABCDEF中,矩形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点,N为CD的中点. 如图,在四棱锥P-ABCD中,ABCD是正方形,PD⊥平面ABCD,PD=AD=2,E,F,G分别是PC,PD,BC的中点.
如图,在四棱锥P-ABCD中,ABCD是正方形,PD⊥平面ABCD,PD=AD=2,E,F,G分别是PC,PD,BC的中点. 如图所示,在五棱锥P-ABCDE中,PE⊥平面ABCDE,DE⊥AE,AB∥DE,BC∥AE.AE=AB=PE=2DE=2BC,F为棱PA的中点,过D、E、F的平面α与棱PB、PC分别交于点G、H.
如图所示,在五棱锥P-ABCDE中,PE⊥平面ABCDE,DE⊥AE,AB∥DE,BC∥AE.AE=AB=PE=2DE=2BC,F为棱PA的中点,过D、E、F的平面α与棱PB、PC分别交于点G、H.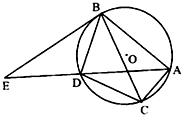 如图,△ABC内接与圆O,AD平分∠BAC交直线BC于点E,交圆O于点D.
如图,△ABC内接与圆O,AD平分∠BAC交直线BC于点E,交圆O于点D. 如图所示,在三棱锥D-ABC中,AB=BC=CD=1,AC=$\sqrt{3}$,平面ACD⊥平面ABC,∠BCD=90°
如图所示,在三棱锥D-ABC中,AB=BC=CD=1,AC=$\sqrt{3}$,平面ACD⊥平面ABC,∠BCD=90°