题目内容
已知二次函数y=f(x)=x2+bx+c的图象过点(1,13),且函数y=f(x-
)是偶函数.
(1)求f(x)的解析式;
(2)已知t<2,g(x)=[f(x)-x2-13]•|x|,求函数g(x)在[t,2]上的最大值和最小值.
| 1 | 2 |
(1)求f(x)的解析式;
(2)已知t<2,g(x)=[f(x)-x2-13]•|x|,求函数g(x)在[t,2]上的最大值和最小值.
分析:(1)根据函数y=f(x-
)是偶函数可求得二次函数f(x)的对称轴方程,从而可求得b;
(2)先把g(x)化为分段函数,作出g(x)的图象,借助图象可直接求得在[t,2]上的最大值,分情况讨论可得g(x)的最小值;
| 1 |
| 2 |
(2)先把g(x)化为分段函数,作出g(x)的图象,借助图象可直接求得在[t,2]上的最大值,分情况讨论可得g(x)的最小值;
解答: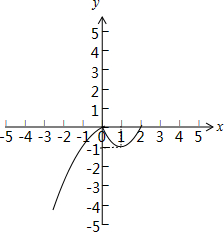 解 (1)因为函数y=f(x-
解 (1)因为函数y=f(x-
)是偶函数,所以二次函数f(x)=x2+bx+c的对称轴方程为x=-
,故b=1.
又因为二次函数f(x)=x2+bx+c的图象过点(1,13),所以1+b+c=13,故c=11.
因此,f(x)的解析式为f(x)=x2+x+11.
(2)g(x)=(x-2)|x|,
当x≤0时,g(x)=-(x-1)2+1,当x>0时,g(x)=(x-1)2-1,作出g(x)的图象,如下图所示:
由图象知,g(x)在[t,2]上的最大值gmax(x)=0,
当1≤t<2时,gmin(x)=t2-2t;当1-
≤t<1时,gmin(x)=-1;当t<1-
时,gmin(x)=-t2+2t;
故g(x)在[t,2]上的最大值为0;最小值gmin(x)=
.
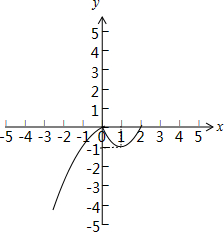 解 (1)因为函数y=f(x-
解 (1)因为函数y=f(x-| 1 |
| 2 |
| 1 |
| 2 |
又因为二次函数f(x)=x2+bx+c的图象过点(1,13),所以1+b+c=13,故c=11.
因此,f(x)的解析式为f(x)=x2+x+11.
(2)g(x)=(x-2)|x|,
当x≤0时,g(x)=-(x-1)2+1,当x>0时,g(x)=(x-1)2-1,作出g(x)的图象,如下图所示:
由图象知,g(x)在[t,2]上的最大值gmax(x)=0,
当1≤t<2时,gmin(x)=t2-2t;当1-
| 2 |
| 2 |
故g(x)在[t,2]上的最大值为0;最小值gmin(x)=
|
点评:本题考查二次函数的性质及二次函数在闭区间上的最值,考查分类讨论思想,属中档题.

练习册系列答案
相关题目
 已知二次函数y=f(x)的图象如图所示:
已知二次函数y=f(x)的图象如图所示: