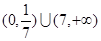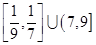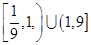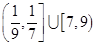题目内容
若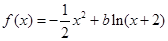 在
在 上是减函数,则
上是减函数,则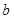 的取值范围是( )
的取值范围是( )
A.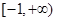 | B. | C.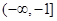 | D.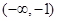 |
C
解析试题分析:因为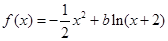 在
在 上是减函数,所以
上是减函数,所以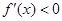 在
在 恒成立,而
恒成立,而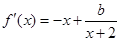 ,所以
,所以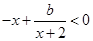 在
在 上恒成立即
上恒成立即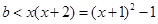 在
在 恒成立,即
恒成立,即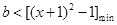 ,因为
,因为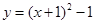 在
在 单调递增,所以
单调递增,所以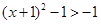 ,从而
,从而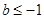 ,(对于
,(对于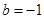 可采用检验法确定,是否可以取到),故选C.
可采用检验法确定,是否可以取到),故选C.
考点:函数的单调性与导数.

练习册系列答案
相关题目
已知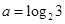 ,
,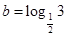 ,
,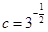 ,则
,则
A.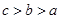 | B.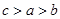 | C.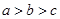 | D.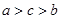 |
指数函数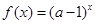 在R上是增函数,则
在R上是增函数,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D.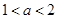 |
如果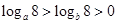 ,那么a、b间的关系是()
,那么a、b间的关系是()
A. | B.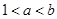 | C.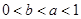 | D.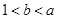 |
函数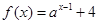 (
( ,且
,且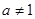 )的图像过一个定点,则这个定点坐标是( )
)的图像过一个定点,则这个定点坐标是( )
| A.(5,1) | B.(1,5) | C.(1,4) | D.(4,1) |
关于x的方程ex-1-|kx|=0(其中e=2.71828…是自然对数的底数)的有三个不同实根,则k的取值范围是
| A.{-2,0,2} | B.(1,+∞) | C.{k|k>e} | D.{k|k2>1} |
设a, b, c均为不等于1的正实数, 则下列等式中恒成立的是
A. |
B. |
C. |
D. |
若 满足
满足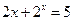 ,
,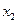 满足
满足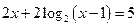 ,则
,则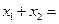 ( )
( )
A.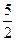 |
| B.3 |
C. |
| D.4 |
 对任意的x满足
对任意的x满足 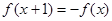 ,当-l≤x<l时,
,当-l≤x<l时, 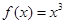 .函数
.函数 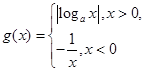 若函数在
若函数在 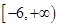 上有6个零点,则实数a的取值范围是( )
上有6个零点,则实数a的取值范围是( )