题目内容
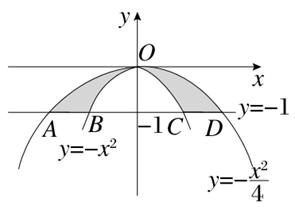
在区间[0,1]上给定曲线 ,如图所示,若使图中的阴影部分的面积
,如图所示,若使图中的阴影部分的面积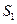 与
与 之和最小,则此区间内的t= 。
之和最小,则此区间内的t= 。
 ,如图所示,若使图中的阴影部分的面积
,如图所示,若使图中的阴影部分的面积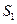 与
与 之和最小,则此区间内的t= 。
之和最小,则此区间内的t= 。
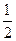
面积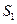 等于边长为t与
等于边长为t与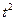 的矩形的面积去掉曲线
的矩形的面积去掉曲线 与x轴、直线x=t围成的面积,即
与x轴、直线x=t围成的面积,即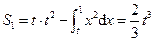 ;面积
;面积 等于曲线
等于曲线 与x轴、x=t,x=1围成的面积去掉矩形面积,矩形边长分别为
与x轴、x=t,x=1围成的面积去掉矩形面积,矩形边长分别为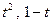 ),即
),即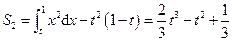 .
.
所以阴影部分面积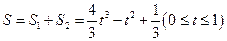 ,
,
由S′(t)=4t2-2t=4t(t-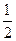 )=0,得t=0或t=
)=0,得t=0或t=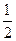 .
.
经验证知,当t=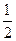 时,S最小.
时,S最小.
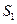 等于边长为t与
等于边长为t与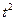 的矩形的面积去掉曲线
的矩形的面积去掉曲线 与x轴、直线x=t围成的面积,即
与x轴、直线x=t围成的面积,即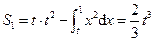 ;面积
;面积 等于曲线
等于曲线 与x轴、x=t,x=1围成的面积去掉矩形面积,矩形边长分别为
与x轴、x=t,x=1围成的面积去掉矩形面积,矩形边长分别为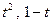 ),即
),即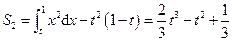 .
.所以阴影部分面积
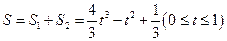 ,
,由S′(t)=4t2-2t=4t(t-
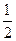 )=0,得t=0或t=
)=0,得t=0或t=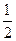 .
.经验证知,当t=
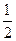 时,S最小.
时,S最小.
练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
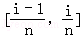



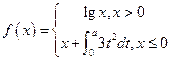 ,若f(f(1))=1,则a=( )
,若f(f(1))=1,则a=( ) 的方向向量为
的方向向量为 且过抛物线
且过抛物线 的焦点,则直线
的焦点,则直线



 x2dx,b=
x2dx,b= 等于( )
等于( )

 则
则 ( )
( )


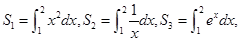 若 ,则s1,s2,s3的大小关系为( )
若 ,则s1,s2,s3的大小关系为( )