题目内容
 某企业有两个生产车间分别在A、B两个位置,A车间有100名员工,B车间有400名员工,现要在公路AC上找一点D,修一条公路BD,并在D处建一个食堂,使得所有员工均在此食堂用餐,已知A、B、C中任意两点间的距离均是1km,设∠BDC=α,所有员工从车间到食堂步行的总路程为S.
某企业有两个生产车间分别在A、B两个位置,A车间有100名员工,B车间有400名员工,现要在公路AC上找一点D,修一条公路BD,并在D处建一个食堂,使得所有员工均在此食堂用餐,已知A、B、C中任意两点间的距离均是1km,设∠BDC=α,所有员工从车间到食堂步行的总路程为S.(1)写出S关于α的函数表达式,并指出α的取值范围;
(2)问食堂D建在距离A多远时,可使总路程S最少?
【答案】分析:(1)在△BCD中先利用正弦定理求得BD,和CD的表达式,进而表示出AD,则总路程S与α的关系可得.
(2)对函数S进行求导,令S'=0求得cosα的值,进而根据导函数判断函数的单调性的方法,可推断出当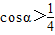 时,当
时,当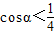 和当
和当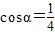 函数的单调性和函数的最小值,进而求得总路程最小时AD的长.
函数的单调性和函数的最小值,进而求得总路程最小时AD的长.
解答:解:(1)在△BCD中,∵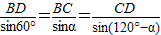 ,
,
∴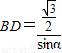 ,
, .
.
则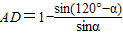 .
.
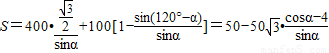 ,其中
,其中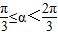 .
.
(2)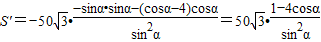
令S'=0,得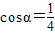 .
.
当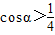 时,S'<0,S是α的单调减函数;
时,S'<0,S是α的单调减函数;
当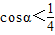 时,S'>0,S是α的单调增函数.
时,S'>0,S是α的单调增函数.
∴当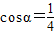 时,S取得最小值.
时,S取得最小值.
此时,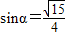 ,
,
 =
=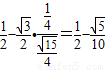 .
.
点评:本题主要考查了基本不等式在最值问题中的应用.考查了学生分析问题和解决实际问题的能力.
(2)对函数S进行求导,令S'=0求得cosα的值,进而根据导函数判断函数的单调性的方法,可推断出当
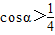 时,当
时,当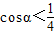 和当
和当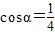 函数的单调性和函数的最小值,进而求得总路程最小时AD的长.
函数的单调性和函数的最小值,进而求得总路程最小时AD的长.解答:解:(1)在△BCD中,∵
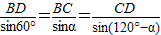 ,
,∴
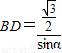 ,
, .
.则
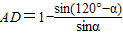 .
.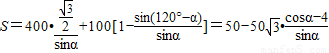 ,其中
,其中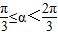 .
.(2)
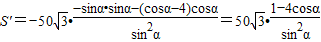
令S'=0,得
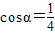 .
.当
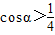 时,S'<0,S是α的单调减函数;
时,S'<0,S是α的单调减函数;当
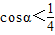 时,S'>0,S是α的单调增函数.
时,S'>0,S是α的单调增函数.∴当
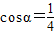 时,S取得最小值.
时,S取得最小值.此时,
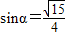 ,
, =
=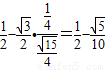 .
.点评:本题主要考查了基本不等式在最值问题中的应用.考查了学生分析问题和解决实际问题的能力.

练习册系列答案
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
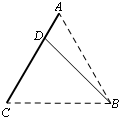 某企业有两个生产车间分别在A、B两个位置,A车间有100名员工,B车间有400名员工,现要在公路AC上找一点D,修一条公路BD,并在D处建一个食堂,使得所有员工均在此食堂用餐,已知A、B、C中任意两点间的距离均是1km,设∠BDC=α,所有员工从车间到食堂步行的总路程为S.
某企业有两个生产车间分别在A、B两个位置,A车间有100名员工,B车间有400名员工,现要在公路AC上找一点D,修一条公路BD,并在D处建一个食堂,使得所有员工均在此食堂用餐,已知A、B、C中任意两点间的距离均是1km,设∠BDC=α,所有员工从车间到食堂步行的总路程为S. 的等边三角形
的等边三角形 的顶点
的顶点 处(如图),现要在边
处(如图),现要在边 上的
上的 点建一仓库,某工人每天用叉车将生产原料从仓库运往车间,同时将成品运回仓库.已知叉车每天要往返
点建一仓库,某工人每天用叉车将生产原料从仓库运往车间,同时将成品运回仓库.已知叉车每天要往返 车间5次,往返
车间5次,往返 车间20次,设叉车每天往返的总路程为
车间20次,设叉车每天往返的总路程为 .(注:往返一次即先从仓库到车间再由车间返回仓库)
.(注:往返一次即先从仓库到车间再由车间返回仓库)
 长为
长为 ,将
,将 表示成
表示成 ,将
,将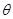 的函数关系式.
的函数关系式. 的最小值,并指出点
的最小值,并指出点 ,所有员工从车间到食堂步行的总路程为S.
,所有员工从车间到食堂步行的总路程为S.
 (1)写出S关于
(1)写出S关于