题目内容
解答时应写出必要的文字说明、证明过程或演算步骤
如图平面ABCD⊥平面ABEF，ABCD是正方形，ABEF是矩形，且AF＝
AD＝2，G是EF的中点，
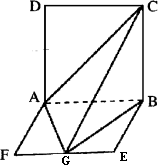
(1)求证平面AGC⊥平面BGC；
(2)求空间四边形AGBC的体积．
答案：
解析：
解析：
|
(1)证明： 从而得： (2)解：由(1)得知：直线CB |
点G是正方形ABEF的边EF的中点．
AG＝BG＝
，
，又因为：平面ABCD
平面ABEF，且
，所以，
平面ABEF，得CB
，
AG
平面BCG，又因为直线AG在平面AGC内，故：平面AGC
平面BGC 7分
平面ABEF，所以，CB是四面体AGBC的高，而：
所以，
14分
练习册系列答案
相关题目
＝(cos
x，sin
＝(
)，且x∈[0，
]．
＋
，求函数f(x)的最值及相应的x的值．
都有f(x)＋f(－x)＝0，且x＝1时，f(x)取极小值
时，
两个实根，(e是自然对数的底数)
)是否存在直线l，使直线l与曲线C交于A，B两点，且
，(O为坐标原点)若存在求出直线l的方程，不存在说明理由．