题目内容
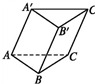 如图,斜三棱柱ABC-A′B′C′中,底面是边长为a的正三角形,侧棱长为b,侧棱AA′与底面相邻两边AB,AC都成45°角.
如图,斜三棱柱ABC-A′B′C′中,底面是边长为a的正三角形,侧棱长为b,侧棱AA′与底面相邻两边AB,AC都成45°角.(Ⅰ)求此斜三棱柱的表面积.
(Ⅱ)求三棱锥B′-ABC的体积.
分析:(Ⅰ)先判断斜三棱柱ABC-A′B′C′的三个侧面的形状,分别求出面积再相加,即为斜三棱柱的侧面积.
(Ⅱ)利用条件求出三棱锥B′-ABC的高,利用三棱锥的体积公式即可求三棱锥的体积.
(Ⅱ)利用条件求出三棱锥B′-ABC的高,利用三棱锥的体积公式即可求三棱锥的体积.
解答:解:(Ⅰ)如图,过A'作A'D⊥平面ABC于点D,过点D作DE⊥AB于点E,DF⊥AC于点F,连接A'E,A'F,AD.
由题意可知∠A'AE=∠A'AF=45°,AA'=AA',
于是Rt△A'AE≌Rt△A'AF.
因此A'E=A'F,从而可得DE=DF.
故AD平分∠BAC,
又∵AB=AC,
∴BC⊥AD.故BC⊥AA'.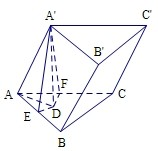
∵AA'∥BB',
∴BC⊥BB'.
因此四边形BCC'B'是矩形,
故斜三棱柱的侧面积为2×a×bsin45°+ab=(
+1)ab.
又∵斜三棱柱的底面积为2×
a2=
a2,
∴斜三棱柱的表面积为(
+1)ab+
a2.
(Ⅱ)由(Ⅰ)可知D为正三角形ABC的中心,
∵正三角形的边长为a,
∴AE=
,AD=
a•
=
,DE=
,
又AE2+DE2=AD2,
即(
b)2+(
)2=(
)2,
解得a=
b,
∴棱棱柱的高为A′D=
=
=
=
=
b,
∴三棱锥B′-ABC的体积等于三棱锥A′-ABC的体积,即
×
a2sin60°×
=
×
×
×
a2b=
a2b.
由题意可知∠A'AE=∠A'AF=45°,AA'=AA',
于是Rt△A'AE≌Rt△A'AF.
因此A'E=A'F,从而可得DE=DF.
故AD平分∠BAC,
又∵AB=AC,
∴BC⊥AD.故BC⊥AA'.

∵AA'∥BB',
∴BC⊥BB'.
因此四边形BCC'B'是矩形,
故斜三棱柱的侧面积为2×a×bsin45°+ab=(
| 2 |
又∵斜三棱柱的底面积为2×
| ||
| 4 |
| ||
| 2 |
∴斜三棱柱的表面积为(
| 2 |
| ||
| 2 |
(Ⅱ)由(Ⅰ)可知D为正三角形ABC的中心,
∵正三角形的边长为a,
∴AE=
| ||
| 2 |
| ||
| 2 |
| 2 |
| 3 |
| ||
| 3 |
| ||
| 6 |
又AE2+DE2=AD2,
即(
| ||
| 2 |
| ||
| 6 |
| ||
| 3 |
解得a=
| 2 |
∴棱棱柱的高为A′D=
| A′A2-A′D2 |
b2-(
|
b2-
|
b2-
|
| ||
| 3 |
∴三棱锥B′-ABC的体积等于三棱锥A′-ABC的体积,即
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 3 |
| 1 |
| 12 |
点评:本题主要考查斜三棱柱的表面积求法以及三棱锥的体积计算,要求熟练掌握常见几何体的体积公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
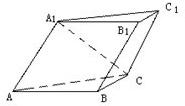 已知如图,斜三棱柱ABC-A1B1C1的侧面A1ACC1与底面ABC垂直,∠ABC=90°,BC=2,AC=2
已知如图,斜三棱柱ABC-A1B1C1的侧面A1ACC1与底面ABC垂直,∠ABC=90°,BC=2,AC=2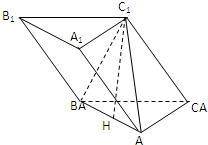 如图,斜三棱柱ABC-A1B1C1中,A1C1⊥BC1,AB⊥AC,AB=3,AC=2,侧棱与底面成60°角.
如图,斜三棱柱ABC-A1B1C1中,A1C1⊥BC1,AB⊥AC,AB=3,AC=2,侧棱与底面成60°角.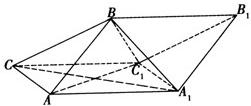 如图,斜三棱柱ABC-A1B1C1的侧面AA1C1C是面积为
如图,斜三棱柱ABC-A1B1C1的侧面AA1C1C是面积为 如图,斜三棱柱ABC-A1B1C1的底面是直角三角形,AC⊥CB,∠ABC=45°,侧面A1ABB1是边长为a的菱形,且垂直于底面ABC,∠A1AB=60°,E、F分别是AB1、BC的中点.
如图,斜三棱柱ABC-A1B1C1的底面是直角三角形,AC⊥CB,∠ABC=45°,侧面A1ABB1是边长为a的菱形,且垂直于底面ABC,∠A1AB=60°,E、F分别是AB1、BC的中点. (2012•潍坊二模)如图,斜三棱柱ABC-A1B1C1,侧面BB1C1C⊥底面ABC,△BC1C是等边三角形,AC⊥BC,AC=BC=4.
(2012•潍坊二模)如图,斜三棱柱ABC-A1B1C1,侧面BB1C1C⊥底面ABC,△BC1C是等边三角形,AC⊥BC,AC=BC=4.