题目内容
某化工厂引进一条先进生产线生产某种化工产品,其生产的总成本 (万元)与年产量
(万元)与年产量 (吨)之间的函数关系式可以近似地表示为
(吨)之间的函数关系式可以近似地表示为 ,已知此生产线年产量最大为210吨。
,已知此生产线年产量最大为210吨。
(1)求年产量为多少吨时,生产每吨产品的平均成本最低,并求每吨产品平均最低成本;
(2)若每吨产品平均出厂价为40万元,那么当年产量为多少吨时,可以获得最大利润?最大利润是多少?
 (万元)与年产量
(万元)与年产量 (吨)之间的函数关系式可以近似地表示为
(吨)之间的函数关系式可以近似地表示为 ,已知此生产线年产量最大为210吨。
,已知此生产线年产量最大为210吨。 (1)求年产量为多少吨时,生产每吨产品的平均成本最低,并求每吨产品平均最低成本;
(2)若每吨产品平均出厂价为40万元,那么当年产量为多少吨时,可以获得最大利润?最大利润是多少?
(1)年产量为200吨时,每吨平均成本最低为32万元;
(2)年产量为210吨时,可获得最大利润1660万元。
(2)年产量为210吨时,可获得最大利润1660万元。
本题考查将实际问题的最值问题转化为函数的最值问题、考查利用基本不等式求函数的最值需满足:一正、二定、三相等、考查求二次函数的最值关键看对称轴
(1)利用总成本除以年产量表示出平均成本;利用基本不等式求出平均成本的最小值.
(2)利用收入减去总成本表示出年利润;通过配方求出二次函数的对称轴;由于开口向下,对称轴处取得最大值.
解:(1)生产每吨产品的平均成本为
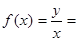
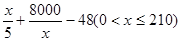 ,
,
由于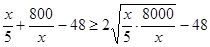
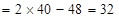 ,
,
当且仅当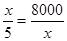 时,即
时,即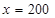 时等号成立。
时等号成立。
答:年产量为200吨时,每吨平均成本最低为32万元;
(2)设年利润为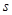 ,则
,则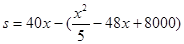
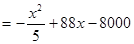
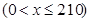
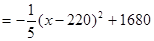 ,
,
由于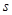 在
在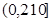 上为增函数,故当
上为增函数,故当
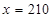 时,
时,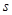 的最大值为1660。
的最大值为1660。
答:年产量为210吨时,可获得最大利润1660万元。
(1)利用总成本除以年产量表示出平均成本;利用基本不等式求出平均成本的最小值.
(2)利用收入减去总成本表示出年利润;通过配方求出二次函数的对称轴;由于开口向下,对称轴处取得最大值.
解:(1)生产每吨产品的平均成本为
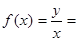
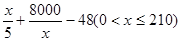 ,
, 由于
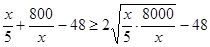
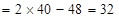 ,
,当且仅当
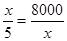 时,即
时,即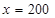 时等号成立。
时等号成立。 答:年产量为200吨时,每吨平均成本最低为32万元;
(2)设年利润为
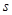 ,则
,则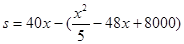
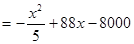
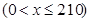
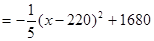 ,
, 由于
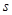 在
在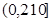 上为增函数,故当
上为增函数,故当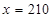 时,
时,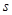 的最大值为1660。
的最大值为1660。答:年产量为210吨时,可获得最大利润1660万元。

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 (其中
(其中 为常数).某人用(0,0),(10,1.1),(30,6.9)求出相关系数,用(60,24.8)验证,请问用以上哪个函数作为模拟函数较好,并说明理由.在一次由这种型号的汽车发生的交通事故中,测得刹车距离为14.4m,问汽车在刹车时的速度大概是多少?
为常数).某人用(0,0),(10,1.1),(30,6.9)求出相关系数,用(60,24.8)验证,请问用以上哪个函数作为模拟函数较好,并说明理由.在一次由这种型号的汽车发生的交通事故中,测得刹车距离为14.4m,问汽车在刹车时的速度大概是多少? ,且
,且 )
)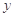 与时间
与时间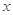 的关系,可选用( )
的关系,可选用( )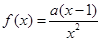 ,其中
,其中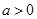 。
。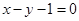 是曲线
是曲线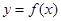 的切线,求a的值;
的切线,求a的值;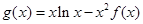 ,求
,求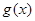 在区间
在区间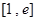 上的最大值。(其中e为自然对数的底数)。
上的最大值。(其中e为自然对数的底数)。 ,②
,② ,③
,③ ,④
,④ ,⑤
,⑤ 中,满足条件“
中,满足条件“ ”的有 .
”的有 . 和
和 构成的面积为200平方米的十字形地域。计划在正方形
构成的面积为200平方米的十字形地域。计划在正方形 上建一座花坛,造价每平方米4200元,并在四周的四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为每平方米210元,再在四个空角上铺草坪,造价为每平方米80元。
上建一座花坛,造价每平方米4200元,并在四周的四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为每平方米210元,再在四个空角上铺草坪,造价为每平方米80元。
 元,
元, 长为
长为 米,试求
米,试求 ,其中
,其中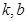 是常数,其图像是一条直线,称这个函数为线性函数,而对于非线性可导函数
是常数,其图像是一条直线,称这个函数为线性函数,而对于非线性可导函数 ,在已知点
,在已知点 附近一点
附近一点 的函数值
的函数值 ,利用这一方法,对于实数
,利用这一方法,对于实数 ,取
,取 ,那么
,那么 ______
______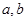 作定义
作定义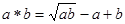 ,若
,若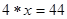 ,则
,则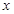 的值是________.
的值是________.