题目内容
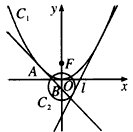
设F是抛物线C1:y2=2px(p>0)的焦点,点A是抛物线与双曲线C2: 的一条渐近线的一个公共点,且AF⊥x轴,则双曲线的离心率为
的一条渐近线的一个公共点,且AF⊥x轴,则双曲线的离心率为
- A.2
- B.

- C.

- D.

D
分析:求出抛物线的焦点坐标和准线方程,利用抛物线的定义 得到 =
= +
+ ,利用离心率的定义求得双曲线的离心率.
,利用离心率的定义求得双曲线的离心率.
解答:由题意得 F( ,0),准线为 x=-
,0),准线为 x=- ,设双曲线的一条渐近线为 y=
,设双曲线的一条渐近线为 y= x,则点A(
x,则点A(  ,
, ),
),
由抛物线的定义得|PF|等于点A到准线的距离,即 =
= +
+ ,
,
∴ =1,e=
=1,e= =
=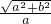 =
= =
= ,
,
故选 D.
点评:本题考查抛物线的定义和双曲线、抛物线的标准方程,以及双曲线、抛物线的简单性质的应用,利用抛物线的定义
得到 =
= +
+ ,是解题的关键.
,是解题的关键.
分析:求出抛物线的焦点坐标和准线方程,利用抛物线的定义 得到
 =
= +
+ ,利用离心率的定义求得双曲线的离心率.
,利用离心率的定义求得双曲线的离心率.解答:由题意得 F(
 ,0),准线为 x=-
,0),准线为 x=- ,设双曲线的一条渐近线为 y=
,设双曲线的一条渐近线为 y= x,则点A(
x,则点A(  ,
, ),
),由抛物线的定义得|PF|等于点A到准线的距离,即
 =
= +
+ ,
,∴
 =1,e=
=1,e= =
=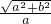 =
= =
= ,
,故选 D.
点评:本题考查抛物线的定义和双曲线、抛物线的标准方程,以及双曲线、抛物线的简单性质的应用,利用抛物线的定义
得到
 =
= +
+ ,是解题的关键.
,是解题的关键. 
练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
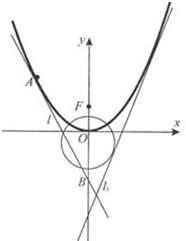 如图,已知直线
如图,已知直线 如图,已知直线
如图,已知直线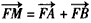 ,则点M在一定直线上,试证明之。
,则点M在一定直线上,试证明之。