题目内容
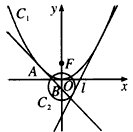
设F是抛物线C1:y2=2px(p>0)的焦点,A是抛物线上一点,且AF⊥x轴,若双曲线C2:
-
=1(a>0,b>0)的一条渐近线也经过A点,则双曲线的渐近线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
分析:依题意可求得A点的坐标,从而可求得双曲线的渐近线方程的斜率,从而可得双曲线的渐近线方程.
解答:解:依题意,抛物线C1:y2=2px(p>0)的交点F(
,0),
∵A是抛物线上一点,且AF⊥x轴,
∴A(
,±P)
又双曲线C2:
-
=1(a>0,b>0)的一条渐近线y=±
也经过A点,
∴kOA=
=±2,
∴
=2,
∴双曲线的渐近线方程为:y=±2x.
故选A.
| p |
| 2 |
∵A是抛物线上一点,且AF⊥x轴,
∴A(
| p |
| 2 |
又双曲线C2:
| x2 |
| a2 |
| y2 |
| b2 |
| b |
| a |
∴kOA=
| ±p | ||
|
∴
| b |
| a |
∴双曲线的渐近线方程为:y=±2x.
故选A.
点评:本题考查抛物线的简单性质与双曲线的简单性质,求得A点的坐标是关键,属于中档题.

练习册系列答案
相关题目
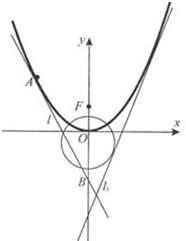 如图,已知直线
如图,已知直线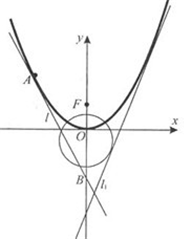 如图,已知直线
如图,已知直线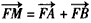 ,则点M在一定直线上,试证明之。
,则点M在一定直线上,试证明之。