Question

【题目】若函数f（x）=x3+a|x2﹣1|，a∈R，则对于不同的实数a，则函数f（x）的单调区间个数不可能是（ ）
A.1个
B.2个
C.3个
D.5个

Answer 1

【答案】B
【解析】解：依题意：（1）当a=0时，f（x）=x3，在（﹣∞，+∞）上为增函数，有一个单调区间①

当a≠0时，∵f（x）=x3+a|x2﹣1|a∈R

∴f（x）=

∴f′（x）= （2）当0＜a＜ 时，∵﹣ ＜﹣ ＜0，0＜ ＜ ，∴导函数的图象如图1：（其中m为图象与x轴交点的横坐标）

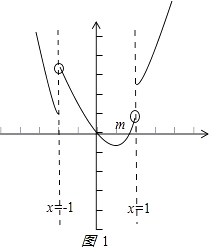
∴x∈（﹣∞，0]时，f′（x）＞0，x∈（0，m）时，f′（x）＜0，x∈[m，+∞）时，f′（x）＞0，

∴f（x）在x∈（﹣∞，0]时，单调递增，x∈（0，m）时，单调递减，x∈[m，+∞）时，单调递增，有3个单调区间②（3）当a≥3时，∵﹣ ＜﹣1， ＞1，∴导函数的图象如图2：（其中n为x≤﹣1时图象与x轴交点的横坐标）

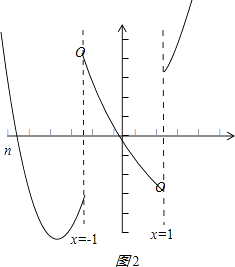
∴x∈（﹣∞，n]时，f′（x）＞0，x∈（n，﹣1]时，f′（x）＜0，x∈（﹣1，0）时，f′（x）＞0，x∈[0，1）时，f′（x）＜0，x∈[1，+∞）时，f′（x）＞0

∴函数f（x）在x∈（﹣∞，n]时，单调递增，x∈（n，﹣1]时，单调递减，x∈（﹣1，0）时，单调递增，x∈[0，1）时，单调递减，x∈[1，+∞）时，单调递增，

有5个单调区间③

由①②③排除A、C、D，

故选B

【考点精析】根据题目的已知条件，利用利用导数研究函数的单调性的相关知识可以得到问题的答案，需要掌握一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减．