题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c,则下列命题正确的是________(写出所有正确命题的序号).
① cosC<1-
cosC<1- cosB;
cosB;
②若acosA=ccosC,则△ABC一定为等腰三角形;
③若A是钝角△ABC中的最大角,则-1<sinA+cosA<1;
④若A= ,a=
,a= ,则b的最大值为2.
,则b的最大值为2.
③④
解析试题分析:
 ,故①错;
,故①错;
因为acosA=ccosC,所以sinAcosA=sinCcosC,所以sin2A=sin2C,可知A=C或者 ,所以△ABC为等腰三角形或直角三角形,故②错;
,所以△ABC为等腰三角形或直角三角形,故②错;
因为 ,
,
所以 ,故③正确;
,故③正确;
因为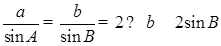 ,又由于
,又由于 ,所以b的最大值为2,故④正确.
,所以b的最大值为2,故④正确.
考点:1.三角恒等变换;2正弦定理.

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
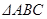 的内角
的内角 的对边分别为
的对边分别为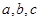 ,且
,且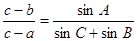 , 则
, 则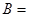 ______
______ ,则A="__________."
,则A="__________."  中,角
中,角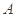 、
、 、
、 的对边分别是
的对边分别是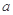 、
、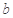 、
、 ,若
,若 ,
, ,
, ,则角
,则角 中,
中, ,
, ,
, ,则
,则
 面积
面积 和三边
和三边 满足:
满足: ,则
,则 ,C=300,BC=3,则AB等于 .
,C=300,BC=3,则AB等于 . ,与观测站A距离
,与观测站A距离  海里的B处有一货船正匀速直线行驶,半小时后,又测得该货船位于观测站A东偏北
海里的B处有一货船正匀速直线行驶,半小时后,又测得该货船位于观测站A东偏北  的C处,且
的C处,且 ,已知A、C两处的距离为10海里,则该货船的船速为海里/小时___________.
,已知A、C两处的距离为10海里,则该货船的船速为海里/小时___________.
 ,AC=1,AB=
,AC=1,AB= ,则BC的长为 .
,则BC的长为 .