题目内容
已知三个数成等差数列,第一第二两数的和的3倍等于第三个数的2倍,如果第二个数减去2,则成等比数列,求这三个数.分析:先根据题意设出着2三个数,进而题意和等比数列的等比中项的性质建立方程组求得a和d,则这三个数可得.
解答:解:设所求之三数为a-d,a,a+d则根据题意有
化简后得
解得:
故所求三数为:
,
,
或1,5,9..
|
化简后得
|
|
|
故所求三数为:
| 1 |
| 4 |
| 5 |
| 4 |
| 9 |
| 4 |
点评:本题主要考查了等比数列和等差数列的性质.作为基础知识的等比数列和等差数列是解决数列问题的基础,应作为重点来掌握.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 为首项为1的等比数列,
为首项为1的等比数列, 为其前项和,已知
为其前项和,已知 三个数成等差数列,则数列
三个数成等差数列,则数列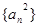 的前5项和为( )
的前5项和为( ) C.1023
D.1024
C.1023
D.1024 为首项为1的等比数列,
为首项为1的等比数列, 为其前
为其前 项和,已知
项和,已知 三个数成等差数列,则数列
三个数成等差数列,则数列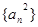 的前5项和为( )
的前5项和为( ) C.1023
D.1024
C.1023
D.1024