题目内容
【题目】已知![]() ,抛物线
,抛物线![]() :
: ![]() 与抛物线
与抛物线![]() :
: ![]() 异于原点
异于原点![]() 的交点为
的交点为![]() ,且抛物线
,且抛物线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)若直线![]() 与抛物线
与抛物线![]() 交于点
交于点![]() ,
, ![]() ,且
,且![]() ,求抛物线
,求抛物线![]() 的方程;
的方程;
(2)证明: ![]() 的面积与四边形
的面积与四边形![]() 的面积之比为定值.
的面积之比为定值.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】试题分析:(1)联立直线方程与抛物线方程,根据弦长公式以及韦达定理得等量关系,求出p,(2)先求M坐标,再求直线![]() 方程,进而求得A,B,C坐标,即得面积,最后作商.
方程,进而求得A,B,C坐标,即得面积,最后作商.
试题解析:(1)解:由![]() ,消去
,消去![]() 得
得![]() .
.
设![]() ,
, ![]() 的坐标分别为
的坐标分别为![]() ,
, ![]() ,
,
则![]() ,
, ![]() .
.
∴![]()
![]() ,∵
,∵![]() ,∴
,∴![]() .
.
故抛物线![]() 的方程为
的方程为![]() .
.
(2)证明:由![]() ,得
,得![]() 或
或![]() ,则
,则![]() .
.
设直线![]() :
: ![]() ,与
,与![]() 联立得
联立得![]() .
.
由![]() ,得
,得![]() ,∴
,∴![]() .
.
设直线![]() :
: ![]() ,与
,与![]() 联立得
联立得![]() .
.
由![]() ,得
,得![]() ,∴
,∴![]() .
.
故直线![]() :
: ![]() ,直线
,直线![]() :
: ![]() ,
,
从而不难求得![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,∴
,∴![]() 的面积与四边形
的面积与四边形![]() 的面积之比为
的面积之比为![]() (为定值).
(为定值).

 名校课堂系列答案
名校课堂系列答案【题目】“中国式过马路”的大意是凑够一撮人即可走,跟红绿灯无关.部分法律专家的观点为“交通规则的制定目的就在于服务城市管理,方便行人,而‘中国式过马路’是对我国法治化进程的严重阻碍,反应了国人规则意识的淡薄.”某新闻媒体对此观点进行了网上调查,所有参与调查的人中,持“支持”“中立”和“不支持”态度的人数如表所示:
支持 | 中立 | 不支持 | |
20岁以下 | 700 | 450 | 200 |
20岁及以上 | 200 | 150 | 300 |
在所有参与调查的人中,用分层随机抽样的方法抽取![]() 人,则持“支持”态度的人中20岁及以上的有_________人
人,则持“支持”态度的人中20岁及以上的有_________人
【题目】2016年1月6日北京时间上午11时30分,朝鲜中央电视台宣布“成功进行了氢弹试验”,再次震动世界,此事件也引起了我国公民热议,其中丹东市(丹东市和朝鲜隔江)某![]() 聊天群有300名网友,乌鲁木齐市某微信群有200名网友,为了解不同地区我国公民对“氢弹试验”事件的关注程度,现采用分层抽样的方法,从中抽取了100名网友,先分别统计了他们在某时段发表的信息条数,再将两地网友发表的信息条数分成5组:
聊天群有300名网友,乌鲁木齐市某微信群有200名网友,为了解不同地区我国公民对“氢弹试验”事件的关注程度,现采用分层抽样的方法,从中抽取了100名网友,先分别统计了他们在某时段发表的信息条数,再将两地网友发表的信息条数分成5组:![]() ,分别加以统计,得到如图所示的频率分布直方图.
,分别加以统计,得到如图所示的频率分布直方图.
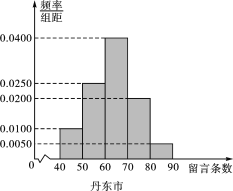
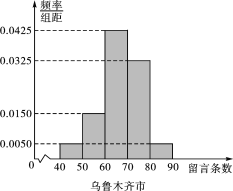
(1)求丹东市网友的平均留言条数(保留整数);
(2)为了进一步开展调查,从样本中留言条数不足50条的网友中随机抽取2人,求至少抽到一名乌鲁木齐市网友的概率;
(3)规定“留言条数”不少于70条为“强烈关注”.
①请你根据已知条件完成下列![]() 的列联表:
的列联表:
强烈关注 | 非强烈关注 | 合计 | |
丹东市 | |||
乌鲁木齐市 | |||
合计 |
②判断是否有![]() 的把握认为“强烈关注”与网友所在的地区有关?
的把握认为“强烈关注”与网友所在的地区有关?
附:临界值表及参考公式:
![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【题目】汕尾市基础教育处为调查在校中学生每天放学后的自学时间情况,在本市的所有中学生中随机抽取了120名学生进行调查,现将日均自学时间小于1小时的学生称为“自学不足”者![]() 根据调查结果统计后,得到如下
根据调查结果统计后,得到如下![]() 列联表,已知在调查对象中随机抽取1人,为“自学不足”的概率为
列联表,已知在调查对象中随机抽取1人,为“自学不足”的概率为![]() .
.
非自学不足 | 自学不足 | 合计 | |
配有智能手机 | 30 | ||
没有智能手机 | 10 | ||
合计 |
![]() 请完成上面的列联表;
请完成上面的列联表;
![]() 根据列联表的数据,能否有
根据列联表的数据,能否有![]() 的把握认为“自学不足”与“配有智能手机”有关?
的把握认为“自学不足”与“配有智能手机”有关?
附表及公式: ![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|