题目内容
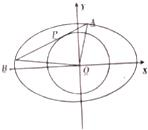 椭圆
椭圆| x2 |
| a2 |
| y2 |
| b2 |
(1)求椭圆的方程;
(2)求
| OA |
| OB |
分析:(1)根据短轴顶点与两焦点的连接组成正三角形可求得b和c的关系,根据点到对应准线的距离等于3可知a和c的关系式,最后联立求得a和b,则椭圆的方程可得.
(2)令P(x0,y0),令A(x1,x2),B(x2,y2),进而可表示l的方程,先看当y0=0时,把直线方程与椭圆方程联立消去y,根据韦达定理得到x1+x2和x1x2的表达式,进而表示出
•
根据x02的范围求得
•
的范围;再看y0=0,x02=1时,可分别求得A,B的坐标,则
•
的值可求得,最后综合可得答案.
(2)令P(x0,y0),令A(x1,x2),B(x2,y2),进而可表示l的方程,先看当y0=0时,把直线方程与椭圆方程联立消去y,根据韦达定理得到x1+x2和x1x2的表达式,进而表示出
| OA |
| OB |
| OA |
| OB |
| OA |
| OB |
解答:解:(1)由题意得
,
求得a=2,b=
,c=1
∴椭圆方程为
+
=1.
(2)令P(x0,y0),因圆的方程为x2+y2=1
∴l的方程为:x0x+y0y=1,令A(x1,x2),B(x2,y2)
①当y0=0时,由
得(3+x02)x2-8x0x+12x20-8=0
∴x1+x2=
,x1x2=
•
=x1x2+y1y2=-
∵0≤x02<1
∴-
≤
•
<-
②当y0=0,x02=1时,可求得A(-1,
),B(-1,-
),或A(1,
),B(1,-
)
此时都有
•
=-
综上-
≤
•
≤-
|
求得a=2,b=
| 3 |
∴椭圆方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)令P(x0,y0),因圆的方程为x2+y2=1
∴l的方程为:x0x+y0y=1,令A(x1,x2),B(x2,y2)
①当y0=0时,由
|
∴x1+x2=
| 8x0 | ||
3+
|
| 12x 20-8 | ||
3+
|
| OA |
| OB |
| 5 | ||
3+
|
∵0≤x02<1
∴-
| 5 |
| 3 |
| OA |
| OB |
| 5 |
| 4 |
②当y0=0,x02=1时,可求得A(-1,
| 3 |
| ,2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
此时都有
| OA |
| OB |
| 5 |
| 4 |
综上-
| 5 |
| 3 |
| OA |
| OB |
| 5 |
| 4 |
点评:本题主要考查了直线与圆锥曲线的综合问题.考查了学生对问题的综合分析和基本的运算能力.

练习册系列答案
相关题目
 如图,椭圆
如图,椭圆 如图,椭圆
如图,椭圆