题目内容
已知二阶矩阵M有特征值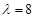 及对应的一个特征向量
及对应的一个特征向量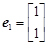 ,并且矩阵M对应的变换将点
,并且矩阵M对应的变换将点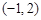 变换成
变换成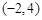 ,求矩阵M..
,求矩阵M..
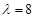 及对应的一个特征向量
及对应的一个特征向量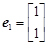 ,并且矩阵M对应的变换将点
,并且矩阵M对应的变换将点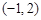 变换成
变换成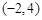 ,求矩阵M..
,求矩阵M..
试题分析:矩阵M的特征值
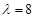 及对应的一个特征向量
及对应的一个特征向量 ,就是有等式
,就是有等式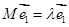 ,矩阵M对应的变换将点
,矩阵M对应的变换将点 变换成
变换成 ,相当于
,相当于 .
.试题解析:设M=
 ,则
,则
 =8
=8 =
= ,故
,故

 =
= ,故
,故
联立以上两方程组解得a=6,b=2,c=4,d=4,故M=
 . 10′
. 10′
练习册系列答案
相关题目
题目内容
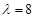 及对应的一个特征向量
及对应的一个特征向量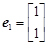 ,并且矩阵M对应的变换将点
,并且矩阵M对应的变换将点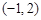 变换成
变换成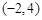 ,求矩阵M..
,求矩阵M..
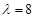 及对应的一个特征向量
及对应的一个特征向量 ,就是有等式
,就是有等式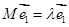 ,矩阵M对应的变换将点
,矩阵M对应的变换将点 变换成
变换成 ,相当于
,相当于 .
. ,则
,则
 =8
=8 =
= ,故
,故

 =
= ,故
,故
 . 10′
. 10′