题目内容
A、B是直线l上的两点，AB=4，AC⊥l于A，BD⊥l于B，AC=BD=3，又AC与BD成60°的角，则C、D两点间的距离是分析：将C．D两点间的距离转化成
的模，表示出
，然后用向量的数量积求解．
| CD |
| CD |
解答：解：
=
+
+
，|
|=|
+
+
|，
CD=
，θ=120°或60°，
CD=
．CD=5或
故答案为：5或
| CD |
| CA |
| AB |
| BD |
| CD |
| CA |
| AB |
| BD |
CD=
| 32+32+42+2× 3×3cosθ |
CD=
| 32+32+42±32 |
| 43 |
故答案为：5或
| 43 |
点评：本题考查空间中两点间的距离，向量的模，是个中档题．
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
状元及第系列答案
同步奥数系列答案
相关题目
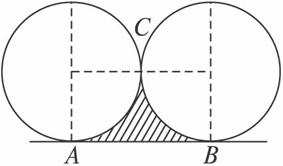
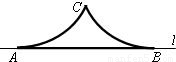
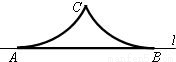
如图，A，B是直线l上的两点，且AB=2．两个半径相等的动圆分别与l相切于A，B点，C是这两个圆的公共点，则圆弧AC，CB与线段AB围成图形面积S的取值范围是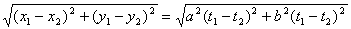
(其中x0,y0,a,b是常数,t是参数)，A，B是直线l上的两个点，它们分别对应参数值t1和t2，那么|AB|等于( )
|t1-t2|
D.|t1|+|t2|
