题目内容
(本小题满分12分)
在△ABC中,角A、B、C的对边分别为a、b、c, 向量 p="(sinA,b+c), " q=(a-c,sinC-sinB),
满足|p +q |="|" p-q |.
(Ⅰ) 求角B的大小;
(Ⅱ)设m=(sin(C+ ),
), ),n="(2k,cos2A)" (k>1), m·n有最大值为3,求k的值.
),n="(2k,cos2A)" (k>1), m·n有最大值为3,求k的值.
解:(Ⅰ)由条件|p +q |="|" p -q |,两边平方得p·q=0,又
p=(sinA,b+c),q=(a-c,sinC-sinB),代入得(a-c)sinA+(b+c)(sinC-sinB)=0,
根据正弦定理,可化为a(a-c)+(b+c)(c-b)=0,
即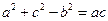 ,又由余弦定理
,又由余弦定理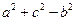 =2acosB,所以cosB=
=2acosB,所以cosB= ,B=
,B=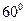 .
.
(Ⅱ)m=(sin(C+ ),
), ),n="(2k,cos2A)" (k>1),
),n="(2k,cos2A)" (k>1),
m·n=2ksin(C+ )+
)+ cos2A="2ksin(C+B)" +
cos2A="2ksin(C+B)" + cos2A
cos2A
=2ksinA+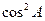 -
- =-
=-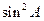 +2ksinA+
+2ksinA+ =-
=-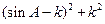 +
+ (k>1).
(k>1).
而0<A<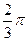 ,sinA∈(0,1],故当sin=1时,m·n取最大值为2k-
,sinA∈(0,1],故当sin=1时,m·n取最大值为2k- =3,得k=
=3,得k=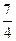 .
.
解析

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
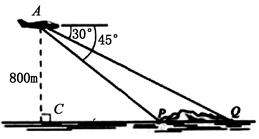
 .
.
 中,角
中,角 所对的边分别为
所对的边分别为 ,向量
,向量 ,且
,且 .
.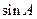 的值;
的值; 
 ,求
,求 .
. 中,角A、B、C所对的边分别为
中,角A、B、C所对的边分别为 、
、 、
、 .已知向量
.已知向量 ,
, ,且
,且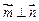 .
. 的大小;
的大小;  ,求边
,求边 的最小值.
的最小值.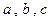 ,
,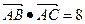 ,
,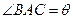 ,
,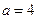 .
.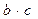 的最大值及
的最大值及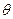 的取值范围;
的取值范围;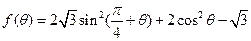 的最值.
的最值. 的面积是30,内角
的面积是30,内角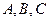 所对边长分别为
所对边长分别为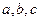 ,
,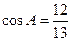 。
。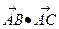 ;
;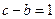 ,求
,求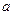 的值。
的值。
 中,
中, ,
, ,
, ,求边
,求边 及
及
 中,已知AB=5,BC=8,
中,已知AB=5,BC=8,
 的值。
的值。