题目内容
【题目】已知抛物线x2=2py(p>0),F为其焦点,过点F的直线l交抛物线于A、B两点,过点B作x轴的垂线,交直线OA于点C,如图所示.
(Ⅰ)求点C的轨迹M的方程;
(Ⅱ)直线m是抛物线的不与x轴重合的切线,切点为P,M与直线m交于点Q,求证:以线段PQ为直径的圆过点F.
【答案】解:(Ⅰ)由题意可得:直线l的斜率存在,设方程为:y=kx+ ![]() , 设A(x1 , y1),B(x2 , y2),动点C(x,y),
, 设A(x1 , y1),B(x2 , y2),动点C(x,y),
由 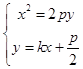 ,可得x2﹣2pkx﹣p2=0.可得x1x2═﹣p2 .
,可得x2﹣2pkx﹣p2=0.可得x1x2═﹣p2 .
OA:y= ![]() =
= ![]() ;OB:x=x2;
;OB:x=x2;
由  可得y=
可得y= ![]() ,
,
即点C的轨迹方程为y=﹣ ![]() .
.
(Ⅱ)证明:设直线m的方程为:y=kx+m,
由 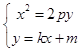 可得x2﹣2pkx﹣2pm=0可得△=4p2k2+8pm,因为直线m与抛物线相切,
可得x2﹣2pkx﹣2pm=0可得△=4p2k2+8pm,因为直线m与抛物线相切,
∴△=0,可得pk2+2m=0,可得P(pk,﹣m),
又由 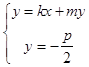 ,可得Q(
,可得Q( ![]() ),
),![]() =(pk,﹣m﹣
=(pk,﹣m﹣ ![]() )(
)( ![]() )
)
=﹣ ![]() (p+2m)+pm+
(p+2m)+pm+ ![]() =0,可得FP⊥FQ,
=0,可得FP⊥FQ,
∴以线段PQ为直径的圆过点F
【解析】(Ⅰ)判断直线l的斜率存在,设方程为:y=kx+ ![]() ,设A(x1 , y1),B(x2 , y2),动点C(x,y)联立直线与抛物线的方程组,利用韦达定理可得x1x2═﹣p2 . 求出OA;OB方程;然后求解轨迹方程.(Ⅱ)设直线m的方程为:y=kx+m,由
,设A(x1 , y1),B(x2 , y2),动点C(x,y)联立直线与抛物线的方程组,利用韦达定理可得x1x2═﹣p2 . 求出OA;OB方程;然后求解轨迹方程.(Ⅱ)设直线m的方程为:y=kx+m,由 ![]() ,得△=4p2k2+8pm,利用直线m与抛物线相切,得P(pk,﹣m),求出Q(
,得△=4p2k2+8pm,利用直线m与抛物线相切,得P(pk,﹣m),求出Q( ![]() ),通过
),通过 ![]() =0,说明以线段PQ为直径的圆过点F.
=0,说明以线段PQ为直径的圆过点F.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目