题目内容
设A={2，-1，a2-a+1}，B={2b，-4，a+4}，M={-1，7}，A∩B=M．
（1）设全集U=A，求CUM；
（2）求a和b的值．
解：（1）∵A∩B=M={-1，7}，∴7∈A，
∴A={2，-1，7}，
∴CUM={2}…（6分）
（2）由（1）得a2-a+1=7，解得a=3或a=-2．
当a=3时，B={2b，-4，7}，此时2b=-1，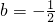
当a=-2时，B={2b，-4，2}，此时不满足A∩B=M={-1，7}，舍去．
综上．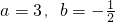
…（12分）
分析：（1）根据集合交集的定义，可知7∈A，从而确定A，再求CUM
（2）由（1）知a2-a+1=7，解得a，再利用集合和元素的关系求b，要注意对求得的值进行验证．
点评：本题考查集合的基本运算，集合和元素的关系．要善于将集合和集合的关系转化为集合和元素的关系．
∴A={2，-1，7}，
∴CUM={2}…（6分）
（2）由（1）得a2-a+1=7，解得a=3或a=-2．
当a=3时，B={2b，-4，7}，此时2b=-1，
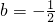
当a=-2时，B={2b，-4，2}，此时不满足A∩B=M={-1，7}，舍去．
综上．
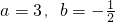…（12分）分析：（1）根据集合交集的定义，可知7∈A，从而确定A，再求CUM
（2）由（1）知a2-a+1=7，解得a，再利用集合和元素的关系求b，要注意对求得的值进行验证．
点评：本题考查集合的基本运算，集合和元素的关系．要善于将集合和集合的关系转化为集合和元素的关系．
练习册系列答案
第三学期赢在暑假系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
);
设A是如下形式的2行3列的数表，
满足性质P：a，b，c，d，e，f∈[-1，1]，且a+b+c+d+e+f=0．
记ri（A）为A的第i行各数之和（i=1，2），Cj（A）为A的第j列各数之和（j=1，2，3）；记k（A）为|r1（A）|，|r2（A）|，|c1（A）|，|c2（A）|，|c3（A）|中的最小值．
（1）对如下数表A，求k（A）的值
（2）设数表A形如
其中-1≤d≤0．求k（A）的最大值；
（Ⅲ）对所有满足性质P的2行3列的数表A，求k（A）的最大值．
| a | b | c |
| d | e | f |
记ri（A）为A的第i行各数之和（i=1，2），Cj（A）为A的第j列各数之和（j=1，2，3）；记k（A）为|r1（A）|，|r2（A）|，|c1（A）|，|c2（A）|，|c3（A）|中的最小值．
（1）对如下数表A，求k（A）的值
| 1 | 1 | -0.8 |
| 0.1 | -0.3 | -1 |
| 1 | 1 | -1-2d |
| d | d | -1 |
（Ⅲ）对所有满足性质P的2行3列的数表A，求k（A）的最大值．