题目内容
设A是如下形式的2行3列的数表,| a | b | c |
| d | e | f |
记ri(A)为A的第i行各数之和(i=1,2),Cj(A)为A的第j列各数之和(j=1,2,3);记k(A)为|r1(A)|,|r2(A)|,|c1(A)|,|c2(A)|,|c3(A)|中的最小值.
(1)对如下数表A,求k(A)的值
| 1 | 1 | -0.8 |
| 0.1 | -0.3 | -1 |
| 1 | 1 | -1-2d |
| d | d | -1 |
(Ⅲ)对所有满足性质P的2行3列的数表A,求k(A)的最大值.
【答案】分析:(1)根据ri(A)为A的第i行各数之和(i=1,2),Cj(A)为A的第j列各数之和(j=1,2,3);记k(A)为|r1(A)|,|r2(A)|,|c1(A)|,|c2(A)|,|c3(A)|中的最小值可求出所求;
(2)k(A)的定义可求出k(A)=1+d,然后根据d的取值范围可求出所求;
(III)任意改变A三维行次序或列次序,或把A中的每个数换成它的相反数,所得数表A*仍满足性质P,并且k(A)=k(A*)
因此,不防设r1(A)≥0,c1(A)≥0,c2(A)≥0,然后利用不等式的性质可知3k(A)≤r1(A)+c1(A)+c2(A),从而求出k(A)的最大值.
解答:解:(1)因为r1(A)=1.2,r2(A)=-1.2,c1(A)=1.1,c2(A)=0.7,c3(A)=-1.8,
所以k(A)=0.7
(2)r1(A)=1-2d,r2(A)=-1+2d,c1(A)=c2(A)=1+d,c3(A)=-2-2d
因为-1≤d≤0,
所以|r1(A)|=|r2(A)|≥1+d≥0,|c3(A)|≥1+d≥0
所以k(A)=1+d≤1
当d=0时,k(A)取得最大值1
(III)任给满足性质P的数表A(如下所示)
任意改变A三维行次序或列次序,或把A中的每个数换成它的相反数,所得数表A*仍满足性质P,并且k(A)=k(A*)
因此,不防设r1(A)≥0,c1(A)≥0,c2(A)≥0,
由k(A)的定义知,k(A)≤r1(A),k(A)≤c1(A),k(A)≤c2(A),
从而3k(A)≤r1(A)+c1(A)+c2(A)=(a+b+c)+(a+d)+(b+e)=(a+b+c+d+e+f)+(a+b-f)=a+b-f≤3
所以k(A)≤1
由(2)可知,存在满足性质P的数表A使k(A)=1,故k(A)的最大值为1.
点评:本题主要考查了进行简单的演绎推理,同时分析问题的能力以及不等式性质的应用,同时考查了转化的思想,属于中档题.
(2)k(A)的定义可求出k(A)=1+d,然后根据d的取值范围可求出所求;
(III)任意改变A三维行次序或列次序,或把A中的每个数换成它的相反数,所得数表A*仍满足性质P,并且k(A)=k(A*)
因此,不防设r1(A)≥0,c1(A)≥0,c2(A)≥0,然后利用不等式的性质可知3k(A)≤r1(A)+c1(A)+c2(A),从而求出k(A)的最大值.
解答:解:(1)因为r1(A)=1.2,r2(A)=-1.2,c1(A)=1.1,c2(A)=0.7,c3(A)=-1.8,
所以k(A)=0.7
(2)r1(A)=1-2d,r2(A)=-1+2d,c1(A)=c2(A)=1+d,c3(A)=-2-2d
因为-1≤d≤0,
所以|r1(A)|=|r2(A)|≥1+d≥0,|c3(A)|≥1+d≥0
所以k(A)=1+d≤1
当d=0时,k(A)取得最大值1
(III)任给满足性质P的数表A(如下所示)
| a | b | c |
| d | e | f |
因此,不防设r1(A)≥0,c1(A)≥0,c2(A)≥0,
由k(A)的定义知,k(A)≤r1(A),k(A)≤c1(A),k(A)≤c2(A),
从而3k(A)≤r1(A)+c1(A)+c2(A)=(a+b+c)+(a+d)+(b+e)=(a+b+c+d+e+f)+(a+b-f)=a+b-f≤3
所以k(A)≤1
由(2)可知,存在满足性质P的数表A使k(A)=1,故k(A)的最大值为1.
点评:本题主要考查了进行简单的演绎推理,同时分析问题的能力以及不等式性质的应用,同时考查了转化的思想,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设A是如下形式的2行3列的数表,
|
a |
b |
c |
|
d |
e |
f |
满足性质P:a,b,c,d,e,f ,且a+b+c+d+e+f=0
,且a+b+c+d+e+f=0
记 为A的第i行各数之和(i=1,2),
为A的第i行各数之和(i=1,2),  为A的第j列各数之和(j=1,2,3)记
为A的第j列各数之和(j=1,2,3)记 为
为 中的最小值。
中的最小值。
(1)对如下表A,求 的值
的值
|
1 |
1 |
-0.8 |
|
0.1 |
-0.3 |
-1 |
(2)设数表A形如
|
1 |
1 |
-1-2d |
|
d |
d |
-1 |
其中 ,求
,求 的最大值
的最大值
(3)对所有满足性质P的2行3列的数表A,求 的最大值。
的最大值。
【解析】(1)因为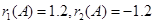 ,
, ,所以
,所以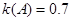
(2)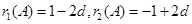 ,
,
因为 ,所以
,所以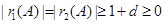 ,
,
所以
当d=0时, 取得最大值1
取得最大值1
(3)任给满足性质P的数表A(如图所示)
|
a |
b |
c |
|
d |
e |
f |
任意改变A的行次序或列次序,或把A中的每个数换成它的相反数,所得数表 仍满足性质P,并且
仍满足性质P,并且 ,因此,不妨设
,因此,不妨设 ,
, ,
,
由 得定义知,
得定义知, ,
, ,
, ,
,
从而

所以, ,由(2)知,存在满足性质P的数表A使
,由(2)知,存在满足性质P的数表A使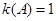 ,故
,故 的最大值为1
的最大值为1
【考点定位】此题作为压轴题难度较大,考查学生分析问题解决问题的能力,考查学生严谨的逻辑思维能力


