题目内容
设直线系M:xcosθ+(y-2)sinθ=1(0≤θ≤2π),对于下列四个结论:(1)当直线垂直y轴时,θ=0或π;
(2)当
 时,直线的倾斜角为120°;
时,直线的倾斜角为120°;(3)M中所有直线均经过一个定点;
(4)存在定点P不在M中的任意一条直线上.
其中正确的是 (写出所有正确的代号)
【答案】分析:(1)当直线垂直y轴时,斜率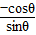 =0,可得θ 的值,从而得到(1)不正确.
=0,可得θ 的值,从而得到(1)不正确.
(2)当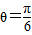 时,求出直线的斜率,从而求出倾斜角为120°,故(2)正确.
时,求出直线的斜率,从而求出倾斜角为120°,故(2)正确.
(3)验证发现,直线系M:xcosθ+(y-2)sinθ=1(0≤θ≤2π)表示圆x2+(y-2)2=1的切线的集合,不会经过定点,
可得(3)不正确.
(4)存在定点P(0,2 )不在M中的任一条直线上,可得(4)正确.
解答:解:直线系M:xcosθ+(y-2)sinθ=1(0≤θ≤2π),即xcosθ+ysinθ-2sinθ-1=0,
(1)当直线垂直y轴时,斜率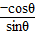 =0,即cosθ=0,可得 θ=
=0,即cosθ=0,可得 θ=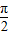 ,或 θ=
,或 θ=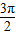 ,故(1)不正确.
,故(1)不正确.
(2)当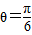 时,直线的斜率等于
时,直线的斜率等于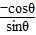 =-
=-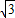 ,故直线的倾斜角为120°,故(2)正确.
,故直线的倾斜角为120°,故(2)正确.
(3)验证发现,直线系M:xcosθ+(y-2)sinθ=1(0≤θ≤2π)表示圆x2+(y-2)2=1的切线的集合,
不会经过定点,故(3)不正确.
(4)存在定点P不在M中的任一条直线上,观察知点P(0,2)即符合条件,故(4)正确.
故答案为 (2)(4).
点评:本题考查直线系方程的应用,依据直线系M表示圆 x2+(y-2)2=1 的切线的集合,本题易因为观察不知直线系所具有的几何特征而导致后两个命题的真假无法判断,对问题进行深入分析是发现其意义的捷径,属于中档题.
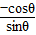 =0,可得θ 的值,从而得到(1)不正确.
=0,可得θ 的值,从而得到(1)不正确.(2)当
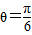 时,求出直线的斜率,从而求出倾斜角为120°,故(2)正确.
时,求出直线的斜率,从而求出倾斜角为120°,故(2)正确.(3)验证发现,直线系M:xcosθ+(y-2)sinθ=1(0≤θ≤2π)表示圆x2+(y-2)2=1的切线的集合,不会经过定点,
可得(3)不正确.
(4)存在定点P(0,2 )不在M中的任一条直线上,可得(4)正确.
解答:解:直线系M:xcosθ+(y-2)sinθ=1(0≤θ≤2π),即xcosθ+ysinθ-2sinθ-1=0,
(1)当直线垂直y轴时,斜率
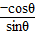 =0,即cosθ=0,可得 θ=
=0,即cosθ=0,可得 θ=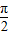 ,或 θ=
,或 θ=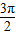 ,故(1)不正确.
,故(1)不正确.(2)当
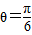 时,直线的斜率等于
时,直线的斜率等于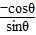 =-
=-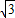 ,故直线的倾斜角为120°,故(2)正确.
,故直线的倾斜角为120°,故(2)正确.(3)验证发现,直线系M:xcosθ+(y-2)sinθ=1(0≤θ≤2π)表示圆x2+(y-2)2=1的切线的集合,
不会经过定点,故(3)不正确.
(4)存在定点P不在M中的任一条直线上,观察知点P(0,2)即符合条件,故(4)正确.
故答案为 (2)(4).
点评:本题考查直线系方程的应用,依据直线系M表示圆 x2+(y-2)2=1 的切线的集合,本题易因为观察不知直线系所具有的几何特征而导致后两个命题的真假无法判断,对问题进行深入分析是发现其意义的捷径,属于中档题.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目